時間序列平滑模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
時間序列平滑模型是指運用時間序列平滑法來構建時間序列的一個基礎模型。時間序列是指將某一現象所發生的數量變化，依時間的先後順序排列，以揭示隨著時間的推移，這一現象的發展規律，從而用以預測現象發展的方向及其數量。
對於平穩時間序列，可以取最近的n項數值的平均值作為下期的預測值。
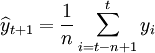
yi為第i期的實際值
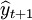為第t+1期的預測值
例 某電子音響器材公司索尼牌單放機的逐月銷售量記錄如下：
簡單移動平均法預測 月份（月） 實際銷售（百台） n=3(百台) n=4(百台) 1 20 2 21 3 23 4 24 21.33 5 25 22.67 21.75 6 27 24. 23.33 7 26 25.33 24.75 8 25 26 25.5 9 26 26 25.75 10 28 26.67 26 11 27 26.33 26.25 12 29 27 26.50
N越大，對干擾的敏感性越低，預測的穩定性越好，響應性就越差。對數據不分遠近，同等對待。
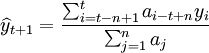
yi為第i期的實際值
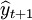為第t+1期的預測值
ai − t + nyi為權重繫數
例 當n=3時，a1=0.5， a2=1.0， a3=1.5，
月份（月） 實際銷售（百台） 加權移動平均法預測 1 20 2 21 3 23 4 24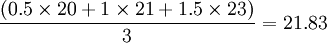 
5 25 23.17 6 27 24.33 7 26 25.83 8 25 26.17 9 26 25.67 10 28 25.67 11 27 26.83 12 29 27.17
n越大，預測的穩定性就好，響應性就越差；n越小，預測的穩定性就越差，響應性就越好。
近期數據的權重越大，則預測的穩定性就越差，響應性就越好；近期數據的權重越小，則預測的穩定性就越好，響應性就越差。
然而，ai和n的選擇都沒有固定的模式，都帶有一定的經驗性，究竟選用什麼數值，要根據預測的實踐而言。
一次指數平滑法的預測公式
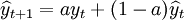
例 某公司的月銷售額記錄，試取a=0.4和0.7,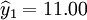
，計算一次指數平滑預測值。
月份（月） 實際銷售額yt ayt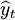 
(1-a)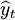
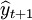
1 10 4 11 6.6 10.6 2 12 3 13 4 16 5 19 6 23 7 26 8 30 9 28 10 18 11 16 12 14
一次指數平滑預測值a=0.7
序號 實際銷售額yt ayt 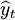(1-a)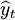
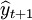
0 10 11 1 12 7 11 3.3 10.3 2 13 8.4 10.3 3.09 11.49 3 16 9.1 11.49 3.45 12.55 4 19 11.2 12.55 3.77 14.97 5 23 13.3 14.97 4.49 17.79 6 26 16.1 17.79 5.34 21.44 7 30 18.2 21.44 6.43 24.63 8 28 21 24.63 7.39 28.39 9 18 19.6 28.39 8.52 28.12 10 16 12.6 28.12 8.44 21.04 11 14 11.2 21.04 6.31 17.51
a選得小一些，預測的穩定性就比較好；反之，響應性比較好。
在有趨勢的情況下，一次指數平滑法預測，會出現滯後現象。
指導思想：歷史上的銷量模式可分解為四組成分：趨勢、季節性波動、周期性變化和殘差（或隨機）波動。
趨勢：銷售的長期變化，原因包括人口變化、企業營銷績效變化、市場對企業產品和服務的接受程度根本變化。
季節性波動指時間序列中規律性的高峰和低谷，通常每12個月重覆一次。造成季節性波動的因素有天氣變化、購買模式隨日曆時間的變化和商品現貨供應情況的變化。 周期性變化：需求模式長期的（超過一年）起伏變化。
殘差（或隨機）波動：總銷售量中不能反映趨勢、季節性或周期性變化的那一部分構成因素.
