時間序列分解模型
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
[編輯]
時間數列分解模型是指運用時間序列分解法構建時間數列的一個基礎模型。時間序列分解法是數年來一直非常有用的方法，反映了經濟現象在一個較長時間內的發展方向。
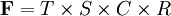
F——需求預測（單位或美元）
T——趨勢水平（單位或美元）
S——季節指數
C——周期指數
R——殘差指數
一般而言，這個模型常常簡化為僅包括趨勢和季節性因素。即周期指數和殘差指數分別為1。
長期趨勢因素（T）反映了經濟現象在一個較長時間內的發展方向，它可以在一個相當長的時間內表現為一種近似直線的持續向上或持續向下或平穩的趨勢。
季節變動因素（S）是經濟現象受季節變動影響所形成的一種長度和幅度固定的周期波動。
周期變動因素(C)也稱迴圈變動因素，它是受各種經濟因素影響形成的上下起伏不定的波動。
不規則變動因素（I）又稱隨機變動，它是受各種偶然因素影響所形成的不規則變動。
時間序列y可以表示為以上四個因素的函數，即：
.
[編輯]
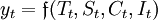時間序列分解的方法有很多，較常用的模型有加法模型和乘法模型。
[編輯]
yt = (Tt + St + Ct + It).
[編輯]
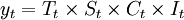
趨勢水平(T)：
線性趨勢線的表達式：T=a+bt
其中t是時間，T是平均需求水平或趨勢，a和b是某時間序列的待定繫數。
[編輯]
1、求趨勢直線方程Tt = a + bt
2、估算季節繫數
| 實際值At | ||
| 趨勢值Tt |
3、預測
已知某旅游服務點過去三年各季度快餐的銷售記錄。試預測該公司未來一年各季度的銷售量。
季度 季度序號t 銷售量At 趨勢值Tt At / Tt 季節繫數 夏 1 11800 10167 1.16 1.15 秋 2 10404 10334 1.01 1.00 冬 3 8925 10501 0.85 0.85 春 4 10600 10668 0.99 1.00 夏 5 12285 10835 1.13 秋 6 11009 11002 1.00 冬 7 9213 11169 0.82 春 8 11286 11336 1.00 夏 9 13350 11503 1.16 秋 10 10270 11670 0.95 冬 11 10266 11837 0.87 春 12 12138 12004 1.01
[編輯]
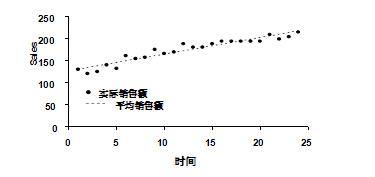
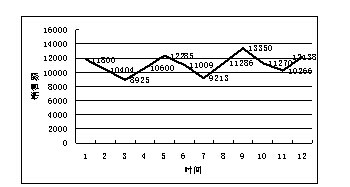
9個數據可以用來分解預測嗎