帕累托分布
出自 MBA智库百科(https://wiki.mbalib.com/)
帕累托分布(Pareto distributions)
目录 |
帕累托分布是以意大利经济学家维弗雷多·帕雷托命名的。 是从大量真实世界的现象中发现的幂次定律分布。这个分布在经济学以外,也被称为布拉德福分布。
帕累托因对意大利20%的人口拥有80%的财产的观察而著名,后来被约瑟夫·朱兰和其他人概括为帕累托法则(80/20法则),后来进一步概括为帕累托分布的概念。
19世纪末期,意大利经济学家维弗雷多·帕累托认为,贫与富的存在,既是经济问题,也有政治原因。
帕累托在研究英国人的收入分配问题时发现,绝大部分社会财富最终总会流向少数人群;他还发现,某一部分人口占总人口的比例,与这一部分人所拥有的财富的份额具有比较确定的计量经济关系;进一步的研究证实,这种不平衡模式可以重复出现,甚至可以预测。经济学把这一社会财富的分布状态,称为“帕累托分布”。
帕累托分布可以归纳为一个非常简洁的表述:通过市场交易,20%的人将占有80%的社会财富,如果交易可以不断进行下去,那么,“在因和果、努力和收获之间,普遍存在着不平衡关系,典型的情况是:80%的收获来自20%的努力;其他 80%的力气只带来20%的结果”。丹尼尔·贝尔在《帕累托分布与收入最大化》中进一步叙述到:“如果待分配的财富总量是100万元,人数为100人,那么我们会有这样一组对应的分配比例:排在前面的20个人,分得80万元;同理,这20人中的4个人,分得64万元;4个人中的1个人,分得50万元。”
如果我们把这些数据用数学公式简单处理一下,就会显示一条收缩中的“财富曲线”以及一条发散中的“贫困曲线”。它的最终走向,是必然会“清零”的,也只有如此,“财富”中所包含的生产力因子才能重新释放出来。
帕累托分布从经济学角度论证出,社会分配的“绝对的失衡”必然导致“绝对的贫困”,甚至导致“宗教末日审判”的来临,除非我们可以通过政治手段,人为地阻止财富向高端不断聚集,否则,贫富双方的利益冲突是不可避免的。
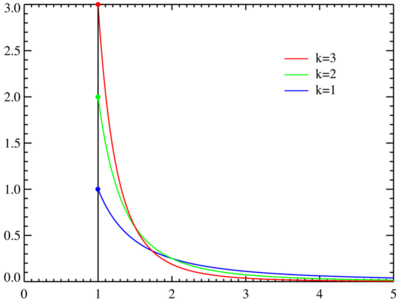
图:帕累托分布 (xmin=1)
在帕累托分布中,如果X是一个随机变量, 则X的概率分布如下面的公式所示:
其中x是任何一个大于xmin的数,xmin是X最小的可能值(正数),k是为正的参数。帕累托分布曲线族是由两个数量参数化的:xmin和k。分布密度则为
帕累托分布属于连续概率分布。
“吉普夫定律”, 也称为“zeta 分布”, 也可以被认为是在离散概率分布中的帕累托分布。 一个遵守帕累托分布的随机变量的期望值为
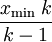 (如果
(如果 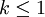 , 期望值为无穷大) 且随机变量的标准差为
, 期望值为无穷大) 且随机变量的标准差为 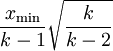 (如果
(如果 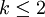 , 标准差不存在)。
, 标准差不存在)。
被认为大致是帕累托分布的例子有:
评论(共10条)
期望的分子不对,多了个k,算了半天。
刚算了一下,期望的计算是对的
很简单的错误,你在计算这个百分比的时候是用了两个值而不是一个统一值。帕累托分布不能在一个数值下解两次,否则结果必然出现你说的问题,原因在于其本身是一个连续概率事件,分解中每个区间呈现递减,而分两次就会产生在一个整体递减的趋势里有一个反向递增趋势的情况。
很简单的错误,你在计算这个百分比的时候是用了两个值而不是一个统一值。帕累托分布不能在一个数值下解两次,否则结果必然出现你说的问题,原因在于其本身是一个连续概率事件,分解中每个区间呈现递减,而分两次就会产生在一个整体递减的趋势里有一个反向递增趋势的情况。
简单点说就是越往后分布得越均匀差别更小,5-20的个体差异大于21-36的个体差异,导致20分的比21的多。在20人里面有16个人分20%是大多数人,80个人里面有16个人分80%是少部分人,不是同样的状态,所以不能像你那么放在一起对比。
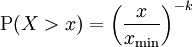
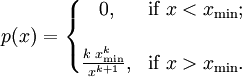








k的倒数具体表示什么意思