帕累托分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
帕累托分佈(Pareto distributions)
目錄 |
帕累托分佈是以義大利經濟學家維弗雷多·帕雷托命名的。 是從大量真實世界的現象中發現的冪次定律分佈。這個分佈在經濟學以外,也被稱為布拉德福分佈。
帕累托因對義大利20%的人口擁有80%的財產的觀察而著名,後來被約瑟夫·朱蘭和其他人概括為帕累托法則(80/20法則),後來進一步概括為帕累托分佈的概念。
19世紀末期,義大利經濟學家維弗雷多·帕累托認為,貧與富的存在,既是經濟問題,也有政治原因。
帕累托在研究英國人的收入分配問題時發現,絕大部分社會財富最終總會流向少數人群;他還發現,某一部分人口占總人口的比例,與這一部分人所擁有的財富的份額具有比較確定的計量經濟關係;進一步的研究證實,這種不平衡模式可以重覆出現,甚至可以預測。經濟學把這一社會財富的分佈狀態,稱為“帕累托分佈”。
帕累托分佈可以歸納為一個非常簡潔的表述:通過市場交易,20%的人將占有80%的社會財富,如果交易可以不斷進行下去,那麼,“在因和果、努力和收穫之間,普遍存在著不平衡關係,典型的情況是:80%的收穫來自20%的努力;其他 80%的力氣只帶來20%的結果”。丹尼爾·貝爾在《帕累托分佈與收入最大化》中進一步敘述到:“如果待分配的財富總量是100萬元,人數為100人,那麼我們會有這樣一組對應的分配比例:排在前面的20個人,分得80萬元;同理,這20人中的4個人,分得64萬元;4個人中的1個人,分得50萬元。”
如果我們把這些數據用數學公式簡單處理一下,就會顯示一條收縮中的“財富曲線”以及一條發散中的“貧困曲線”。它的最終走向,是必然會“清零”的,也只有如此,“財富”中所包含的生產力因數才能重新釋放出來。
帕累托分佈從經濟學角度論證出,社會分配的“絕對的失衡”必然導致“絕對的貧困”,甚至導致“宗教末日審判”的來臨,除非我們可以通過政治手段,人為地阻止財富向高端不斷聚集,否則,貧富雙方的利益衝突是不可避免的。
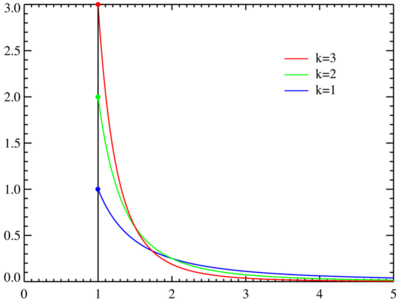
圖:帕累托分佈 (xmin=1)
在帕累托分佈中,如果X是一個隨機變數, 則X的概率分佈如下麵的公式所示:
其中x是任何一個大於xmin的數,xmin是X最小的可能值(正數),k是為正的參數。帕累托分佈曲線族是由兩個數量參數化的:xmin和k。分佈密度則為
帕累托分佈屬於連續概率分佈。
“吉普夫定律”, 也稱為“zeta 分佈”, 也可以被認為是在離散概率分佈中的帕累托分佈。 一個遵守帕累托分佈的隨機變數的期望值為
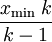 (如果
(如果 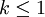 , 期望值為無窮大) 且隨機變數的標準差為
, 期望值為無窮大) 且隨機變數的標準差為 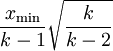 (如果
(如果 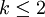 , 標準差不存在)。
, 標準差不存在)。
被認為大致是帕累托分佈的例子有:
評論(共10條)
期望的分子不對,多了個k,算了半天。
剛算了一下,期望的計算是對的
很簡單的錯誤,你在計算這個百分比的時候是用了兩個值而不是一個統一值。帕累托分佈不能在一個數值下解兩次,否則結果必然出現你說的問題,原因在於其本身是一個連續概率事件,分解中每個區間呈現遞減,而分兩次就會產生在一個整體遞減的趨勢里有一個反向遞增趨勢的情況。
很簡單的錯誤,你在計算這個百分比的時候是用了兩個值而不是一個統一值。帕累托分佈不能在一個數值下解兩次,否則結果必然出現你說的問題,原因在於其本身是一個連續概率事件,分解中每個區間呈現遞減,而分兩次就會產生在一個整體遞減的趨勢里有一個反向遞增趨勢的情況。
簡單點說就是越往後分佈得越均勻差別更小,5-20的個體差異大於21-36的個體差異,導致20分的比21的多。在20人裡面有16個人分20%是大多數人,80個人裡面有16個人分80%是少部分人,不是同樣的狀態,所以不能像你那麼放在一起對比。
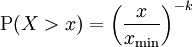
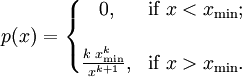








k的倒數具體表示什麼意思