Pooled MLE模型
出自 MBA智库百科(https://wiki.mbalib.com/)
Pooled MLE模型(Pooled MLE Model)
目錄 |
1997年R. Carter Hill、J. R. Knight、C. F. Sirmans對Pooled GLS模型進行了改進,提出基於最大似然估計法(MLE)的Pooled MLE模型。
假設共有N+NR宗房地產的價格數據,其中N個數據是Hedonic數據,即房地產只出售過一次。其餘NR宗房地產屬於重覆售出樣本,同一宗房地產有一次以上的價格資料。
由於存在多重共線性,不失一般性,對於Hedonic數據,假設:
vit = ρvit − 1 + uit
其中ρ為自相關係數,|ρ|<1。進一步假設uit具有異方差性,Vae(uit) = σ2i
因此有:
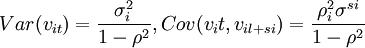
對於重覆售出數據,隨機誤差項ei = Vit + si − Vit有方差;
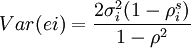
假設誤差Vit和ei服從正態分佈,則N+NR個樣本的似然函數為L=L1+L2,其中:
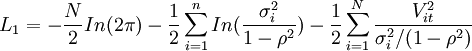
是N個Hedonic數據的對數似然函數。而
![L_2=-\frac{N_R}{2}In(2\pi)-\frac{1}{2}\sum^{n_R}_{i=1}In\left[\frac{2\sigma^2_i(1-\rho^{si})}{1-\rho^2}\right]-\frac{1-\rho^2}{2}\sum^{N_R}_{i=1}\frac{e^2_i}{2\sigma^2_i(1-\rho^{si})}](/w/images/math/3/a/f/3af70114115063f30f58e88777328401.png)
則是NR個重覆售出數據的對數似然函數。令L→∞,估計出方差σi2和自相關係數ρ,然後再估計出混合模型中的所有未知參數。
Hill等利用隨機模擬實驗表明採用Pooled MLE模型估計房地產價格指數,比其他模型有更小的漸近方差。
Pooled MLE模型的特點是:
(1)Hedonic模型和重覆售出模型的數據都可用,價格數據資料比較容易獲得,抽樣誤差較小;
(2)剋服了重覆售出模型的缺陷,可估計出折舊繫數;
(3)剋服了Hedonic模型的缺陷,合理地考慮了序列相關問題,使估計效果比其它各種模型更為優越;
(4)由於對數似然函數L是非線性的,估計參數的計算較為複雜,需要進行演算法分析,但現成的軟體包,如SHAZ AM,LIMDEP和GAUSS等可以幫助運算。







