Pooled MLE模型
出自 MBA智库百科(https://wiki.mbalib.com/)
Pooled MLE模型(Pooled MLE Model)
目录 |
1997年R. Carter Hill、J. R. Knight、C. F. Sirmans对Pooled GLS模型进行了改进,提出基于最大似然估计法(MLE)的Pooled MLE模型。
假设共有N+NR宗房地产的价格数据,其中N个数据是Hedonic数据,即房地产只出售过一次。其余NR宗房地产属于重复售出样本,同一宗房地产有一次以上的价格资料。
由于存在多重共线性,不失一般性,对于Hedonic数据,假设:
vit = ρvit − 1 + uit
其中ρ为自相关系数,|ρ|<1。进一步假设uit具有异方差性,Vae(uit) = σ2i
因此有:
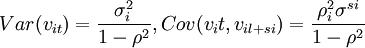
对于重复售出数据,随机误差项ei = Vit + si − Vit有方差;
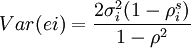
假设误差Vit和ei服从正态分布,则N+NR个样本的似然函数为L=L1+L2,其中:
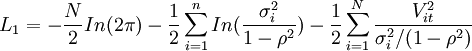
是N个Hedonic数据的对数似然函数。而
![L_2=-\frac{N_R}{2}In(2\pi)-\frac{1}{2}\sum^{n_R}_{i=1}In\left[\frac{2\sigma^2_i(1-\rho^{si})}{1-\rho^2}\right]-\frac{1-\rho^2}{2}\sum^{N_R}_{i=1}\frac{e^2_i}{2\sigma^2_i(1-\rho^{si})}](/w/images/math/3/a/f/3af70114115063f30f58e88777328401.png)
则是NR个重复售出数据的对数似然函数。令L→∞,估计出方差σi2和自相关系数ρ,然后再估计出混合模型中的所有未知参数。
Hill等利用随机模拟实验表明采用Pooled MLE模型估计房地产价格指数,比其他模型有更小的渐近方差。
Pooled MLE模型的特点是:
(1)Hedonic模型和重复售出模型的数据都可用,价格数据资料比较容易获得,抽样误差较小;
(2)克服了重复售出模型的缺陷,可估计出折旧系数;
(3)克服了Hedonic模型的缺陷,合理地考虑了序列相关问题,使估计效果比其它各种模型更为优越;
(4)由于对数似然函数L是非线性的,估计参数的计算较为复杂,需要进行算法分析,但现成的软件包,如SHAZ AM,LIMDEP和GAUSS等可以帮助运算。







