單因素方差分析

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自Oneway ANOVA)

單因素方差分析（One Way ANOVA）

什麼是單因素方差分析

　　單因素方差分析是指對單因素試驗結果進行分析，檢驗因素對試驗結果有無顯著性影響的方法。

　　單因素方差分析是兩個樣本平均數比較的引伸，它是用來檢驗多個平均數之間的差異，從而確定因素對試驗結果有無顯著性影響的一種統計方法。

[編輯]

單因素方差分析相關概念

因素：影響研究對象的某一指標、變數。
水平：因素變化的各種狀態或因素變化所分的等級或組別。
單因素試驗：考慮的因素只有一個的試驗叫單因素試驗。

[編輯]

單因素方差分析示例^[1]

　　例如，將抗生素註入人體會產生抗生素與血漿蛋白質結合的現象，以致減少了藥效。下表列出了5種常用的抗生素註入到牛的體內時，抗生素與血漿蛋白質結合的百分比。現需要在顯著性水平 $α = 0.05$ 下檢驗這些百分比的均值有無顯著的差異。設各總體服從正態分佈，且方差相同。

青黴素	四環素	鏈黴素	紅黴素	氯黴素
29.6	27.3	5.8	21.6	29.2
24.3	32.6	6.2	17.4	32.8
28.5	30.8	11.0	18.3	25.0
32.0	34.8	8.3	19.0	24.2

　　在這裡，試驗的指標是抗生素與血漿蛋白質結合的百分比，抗生素為因素，不同的5種抗生素就是這個因素的五個不同的水平。假定除抗生素這一因素外，其餘的一切條件都相同。這就是單因素試驗。試驗的目的是要考察這些抗生素與血漿蛋白質結合的百分比的均值有無顯著的差異。即考察抗生素這一因素對這些百分比有無顯著影響。這就是一個典型的單因素試驗的方差分析問題。

　　與通常的統計推斷問題一樣，方差分析的任務也是先根據實際情況提出原假設 $H 0$ 與備擇假設 $H 1$ ，然後尋找適當的檢驗統計量進行假設檢驗。本節將借用上面的實例來討論單因素試驗的方差分析問題。

　　在上例中，因素A（即抗生素）有s（=5）個水平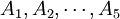 $A_1,A_2,\cdots,A_5$ ，在每一個水平 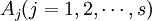$A_j(j=1,2,\cdots,s)$ 下進行了 $n j = 4$ 次獨立試驗，得到如上表所示的結果。這些結果是一個隨機變數。表中的數據可以看成來自s個不同總體（每個水平對應一個總體）的樣本值，將各個總體的均值依次記為 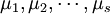$\mu_1,\mu_2,\cdots,\mu_s$ ,則按題意需檢驗假設

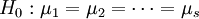
　　 $H_0:\mu_1=\mu_2=\cdots=\mu_s$

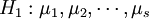　　 $H_1:\mu_1,\mu_2,\cdots,\mu_s$ 不全相等

為了便於討論，現在引入總平均 $μ$

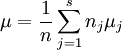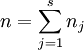
　　 $\mu=\frac{1}{n}\sum_{j=1}^s n_j \mu_j$ 其中： $n=\sum_{j=1}^s n_j$

再引入水平 $A j$ 的效應 $δ j$

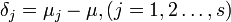
$\delta_j=\mu_j-\mu,(j=1,2\ldots,s)$

顯然有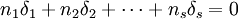 $n_1\delta_1+n_2\delta_2+\cdots+n_s\delta_s=0$ ， $δ j$ 表示水平 $A j$ 下的總體平均值與總平均的差異。

利用這些記號，本例的假設就等價於假設

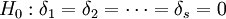
　　 $H_0:\delta_1=\delta_2=\cdots=\delta_s=0$

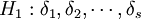　　 $H_1:\delta_1,\delta_2,\cdots,\delta_s$ 不全為零

因此，單因素方差分析的任務就是檢驗s個總體的均值 $μ j$ 是否相等，也就等價於檢驗各水平 $A j$ 的效應 $δ j$ 是否都等於零。

　　2. 檢驗所需的統計量

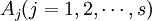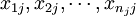　　假設各總體服從正態分佈，且方差相同，即假定各個水平 $A_j(j=1,2,\cdots,s)$ 下的樣本 $x_{1j},x_{2j},\cdots,x_{n_jj}$ 來自正態總體 $N (μ j,σ 2)$ ， $μ j$ 與 $σ 2$ 未知，且設不同水平 $A j$ 下的樣本之間相互獨立，則單因素方差分析所需的檢驗統計量可以從總平方和的分解導出來。下麵先引入：

　　水平 $A j$ 下的樣本平均值:

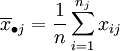
　　 ${\overline x}_{\bullet j}=\frac{1}{n}\sum_{i=1}^{n_j}x_{ij}$

　　數據的總平均:

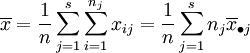
　　 $\overline{x}=\frac{1}{n}\sum_{j=1}^s\sum_{i=1}^{n_j}x_{ij}=\frac{1}{n}\sum_{j=1}^sn_j{\overline x}_{\bullet j}$

　　總平方和:

　　 $S_T=\sum_{j=1}^s \sum_{i=1}^{n_j}{(x_{ij}-\overline x)}^2$

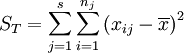
總平方和 $S T$ 反映了全部試驗數據之間的差異，因此 $S T$ 又稱為總變差。將其分解為

　　 $S T = S E + S A$

其中:

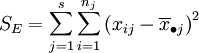
　　 $S_E=\sum_{j=1}^s \sum_{i=1}^{n_j}{(x_{ij}\overline x}_{\bullet j})}^2$

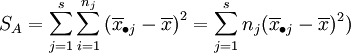
　　 $S_A=\sum_{j=1}^s \sum_{i=1}^{n_j}{({\overline x}_{\bullet j\overline x)}^2=\sum_{j=1}^s n_j({\overline x}_{\bullet j}-\overline x)^2)$

上述 $S E$ 的各項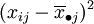 $(x_{ij}\overline x}_{\bullet j})^2$ 表示了在水平 $A j$ 下，样本观察值与样本均值的差异，这是由随机误差所引起的，因此 $S E$ 叫做误差平方和。 $S A$ 的各项 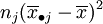$n_j({\overline x}_{\bullet j\overline x)^2$ 表示了在水平 $A j$ 下的樣本平均值與數據總平均的差異，這是由水平 $A j$ 以及隨機誤差所引起的，因此 $S A$ 叫做因素A的效應平方和。

　　可以證明 $S A$ 與 $S E$ 相互獨立，且當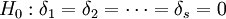 $H_0:\delta_1=\delta_2=\cdots=\delta_s=0$ 為真時， $S A$ 與 $S E$ 分別服從自由度為 $s - 1, n - s$ 的 $χ 2$ 分佈，即

　　 $S A / σ 2 ˜χ 2 (s - 1)$

　　 $S E / σ 2 ˜χ 2 (n - s)$

於是，當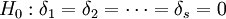 $H_0:\delta_1=\delta_2=\cdots=\delta_s=0$ 為真時

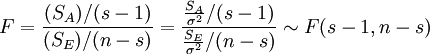
　　 $F=\frac{(S_A)/(s-1)}{(S_E)/(n-s)}=\frac{\frac{S_A}{\sigma^2}/(s-1)}{\frac{S_E}{\sigma^2}/(n-s)} \sim F(s-1,n-s)$

這就是單因素方差分析所需的服從F分佈的檢驗統計量。

　　3. 假設檢驗的拒絕域

　　通過上面的分析可得，在顯著性水平 $α$ 下，本檢驗問題的拒絕域為

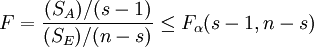
　　 $F=\frac{(S_A)/(s-1)}{(S_E)/(n-s)}\le F_{\alpha}(s-1,n-s)$

為了方便分析比較，通常將上述分析結果編排成如下表所示的方差分析表。表中的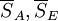 $\overline S_A,\overline S_E$ 分別稱為 $S A, S E$ 的均方。

方差來源	平方和	自由度	均方	F比
因素A	$S A$	$s - 1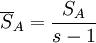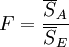$	$\overli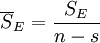ne S_A=\frac{S_A}{s-1}$	$F=\frac{\overline S_A}{\overline S_E}$
誤差	$S E$	$n - s$	$\overline S_E=\frac{S_E}{n-s}$
總和	$S T$	$n - 1$

[編輯]

參考文獻

↑ 趙丹亞，邵麗.中文版Excel2000應用案例.人民郵電出版社,2000年01月第1版

取自"https://wiki.mbalib.com/zh-tw/%E5%8D%95%E5%9B%A0%E7%B4%A0%E6%96%B9%E5%B7%AE%E5%88%86%E6%9E%90"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Cabbage,Zfj3000,Vulture,HEHE林,泡芙小姐,Llyn.

頁面分類: 統計方法

評論(共6條)

提示:評論內容為網友針對條目"單因素方差分析"展開的討論，與本站觀點立場無關。

129.34.20.* 在 2012年2月27日 10:20 發表

本文有錯誤，特別是總變差的公式，組間變差和等，容易誤導人。請更正。

回複評論

123.117.34.* 在 2013年5月24日 17:00 發表

最後給出的拒絕域是錯誤的吧，應該是F>F阿爾法是拒絕域，P值小於顯著性水平時也拒絕原假設

回複評論

222.178.202.* 在 2014年12月9日 11:23 發表

好！

回複評論

117.162.193.* 在 2021年5月13日 09:17 發表

統計學太難了

回複評論

183.246.21.* 在 2021年7月5日 20:05 發表

總變差公式錯誤。此時仍未改正

回複評論

Llyn (討論 | 貢獻) 在 2021年7月6日 09:41 發表

183.246.21.* 在 2021年7月5日 20:05 發表

總變差公式錯誤。此時仍未改正

我看了下，稍微修改了，如果你還發現別的錯誤，歡迎直接修改編輯！

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

單因素方差分析

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是單因素方差分析

單因素方差分析相關概念

單因素方差分析示例^[1]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共6條)

導航

意见反馈

查看

工具▼

單因素方差分析

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是單因素方差分析

單因素方差分析相關概念

單因素方差分析示例[1]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共6條)

導航

意见反馈

單因素方差分析示例^[1]