Dijkstra演算法
出自 MBA智库百科(https://wiki.mbalib.com/)
Dijkstra演算法(狄克斯特拉演算法)
目錄 |
Dijkstra演算法是由荷蘭電腦科學家狄克斯特拉(Dijkstra)於1959 年提出的,因此又叫狄克斯特拉演算法。是從一個頂點到其餘各頂點的最短路徑演算法,解決的是有向圖中最短路徑問題。
其基本原理是:每次新擴展一個距離最短的點,更新與其相鄰的點的距離。當所有邊權都為正時,由於不會存在一個距離更短的沒擴展過的點,所以這個點的距離永遠不會再被改變,因而保證了演算法的正確性。不過根據這個原理,用Dijkstra求最短路的圖不能有負權邊,因為擴展到負權邊的時候會產生更短的距離,有可能就破壞了已經更新的點距離不會改變的性質。
舉例來說,如果圖中的頂點表示城市,而邊上的權重表示著城市間開車行經的距離。 Dijkstra演算法可以用來找到兩個城市之間的最短路徑。
Dijkstra演算法的輸入包含了一個有權重的有向圖G,以及G中的一個來源頂點S。 我們以V表示G中所有頂點的集合。 每一個圖中的邊,都是兩個頂點所形成的有序元素對。(u,v)表示從頂點u到v有路徑相連。 我們以E所有邊的集合,而邊的權重則由權重函數w: E → [0, ∞]定義。 因此,w(u,v)就是從頂點u到頂點v的非負花費值(cost)。 邊的花費可以想像成兩個頂點之間的距離。任兩點間路徑的花費值,就是該路徑上所有邊的花費值總和。 已知有V中有頂點s及t,Dijkstra演算法可以找到s到t的最低花費路徑(i.e. 最短路徑)。 這個演算法也可以在一個圖中,找到從一個頂點s到任何其他頂點的最短路徑。
這個演算法是通過為每個頂點v保留目前為止所找到的從s到v的最短路徑來工作的。初始時,源點s的路徑長度值被賦為0(d[s]=0), 同時把所有其他頂點的路徑長度設為無窮大,即表示我們不知道任何通向這些頂點的路徑(對於V中所有頂點v除s外d[v]= ∞)。當演算法結束時,d[v]中儲存的便是從s到v的最短路徑,或者如果路徑不存在的話是無窮大。 Dijstra演算法的基礎操作是邊的拓展:如果存在一條從u到v的邊,那麼從s到u的最短路徑可以通過將邊(u,v)添加到尾部來拓展一條從s到v的路徑。這條路徑的長度是d[u]+w(u,v)。如果這個值比目前已知的d[v]的值要小,我們可以用新值來替代當前d[v]中的值。拓展邊的操作一直執行到所有的d[v]都代表從s到v最短路徑的花費。這個演算法經過組織因而當d[u]達到它最終的值的時候沒條邊(u,v)都只被拓展一次。
演算法維護兩個頂點集S和Q。集合S保留了我們已知的所有d[v]的值已經是最短路徑的值頂點,而集合Q則保留其他所有頂點。集合S初始狀態為空,而後每一步都有一個頂點從Q移動到S。這個被選擇的頂點是Q中擁有最小的d[u]值的頂點。當一個頂點u從Q中轉移到了S中,演算法對每條外接邊(u,v)進行拓展。
在下麵的演算法中,u:=Extract_Min(Q)在在頂點集Q中搜索有最小的d[u]值的頂點u。這個頂點被從集合Q中刪除並返回給用戶。
1 function Dijkstra(G, w, s)
2 for each vertex v in V[G] // 初始化
3 d[v] := infinity
4 previous[v] := undefined
5 d[s] := 0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijstra演算法主體
9 u := Extract_Min(Q)
10 S := S union {u}
11 for each edge (u,v) outgoing from u
12 if d[v] > d[u] + w(u,v) // 拓展邊(u,v)
13 d[v] := d[u] + w(u,v)
14 previous[v] := u
如果我們只對在s和t之間尋找一條最短路徑的話,我們可以在第9行添加條件如果滿足u=t的話終止程式。
現在我們可以通過迭代來回溯出s到t的最短路徑
1 S := empty sequence 2 u := t 3 while defined u 4 insert u to the beginning of S 5 u := previous[u]
現在序列S就是從s到t的最短路徑的頂點集.
我們可以用大O符號將Dijkstra演算法的運行時間表示為邊數m和頂點數n的函數。
Dijkstra演算法最簡單的實現方法是用一個鏈表或者數組來存儲所有頂點的集合Q,所以搜索Q中最小元素的運算(Extract-Min(Q))只需要線性搜索Q中的所有元素。這樣的話演算法的運行時間是O(n2)。
對於邊數少於n2稀疏圖來說,我們可以用鄰接表來更有效的實現Dijkstra演算法。同時需要將一個二叉堆或者斐波納契堆用作優先隊列來尋找最小的頂點(Extract-Min)。當用到二叉堆的時候,演算法所需的時間為O((m+n)log n),斐波納契堆能稍微提高一些性能,讓演算法運行時間達到O(m + n log n)。 相關問題和演算法
在Dijkstra演算法的基礎上作一些改動,可以擴展其功能。例如,有時希望在求得最短路徑的基礎上再列出一些次短的路徑。為此,可先在原圖上計算出最短路徑,然後從圖中刪去該路徑中的某一條邊,在餘下的子圖中重新計算最短路徑。對於原最短路徑中的每一條邊,均可求得一條刪去該邊後子圖的最短路徑,這些路徑經排序後即為原圖的一系列次短路徑。
OSPF(open shortest path first, 開放最短路徑優先)演算法是Dijkstra演算法在網路路由中的一個具體實現。
與Dijkstra演算法不同,Bellman-Ford演算法可用於具有負花費邊的圖,只要圖中不存在總花費為負值且從源點 s 可達的環路(如果有這樣的環路,則最短路徑不存在,因為沿環路迴圈多次即可無限制的降低總花費)。
與最短路徑問題有關的一個問題是旅行商問題(traveling salesman problem),它要求找出通過所有頂點恰好一次且最終回到源點的最短路徑。該問題是NP難的;換言之,與最短路徑問題不同,旅行商問題不太可能具有多項式時間演算法。
如果有已知信息可用來估計某一點到目標點的距離,則可改用A*演算法,以減小最短路徑的搜索範圍。
案例一:基於Dijkstra演算法在物流配送中的應用[1]
電子商務是依托於互聯網和信息技術的一種新型商務活動。目前,我國的電子商務發展勢頭迅猛,已經成為國民經濟中的重要組成部分。相對於新生的電子商務來說,物流配送出現得比較早但是真正把它當作一個完整的系統來研究還是在20世紀50年代初。
在電子商務尤其是B2C業務開展之初,國內還沒有一家物流公司具有電子商務的配送經驗,各個電子商務公司只能求助於具有國內最大覆蓋網路的中國郵政速遞公司,EMS但是在經歷一段時間之後,EMS由於自身體制的僵化分割,管理無法協調、服務水平無法提高、費用居高不下,對很多問題都是心有餘而力不足,無法滿足電子商務發展的快速要求。
鑒於此種情景,國內的許多大型電子商務公司都在積極地尋找出路,有的自己投資組建配送隊伍,但是要將自己的網點覆蓋全國實在太難、投資太大有的積極尋找新近進人電子商務配送領域的配送公司,但是後來者的實力和發展速度著實無法滿足需求也有求助傳統的第三方物流公司,在電子商務覆蓋需求如此廣大,服務環節如此複雜,業務特點往往品種多、數量少、利潤低等實際問題面前,傳統的物流公司往往是望而卻步。
商品配送成本過高電子商務公司的配送不僅面向批發商和零售商,還要直接面對大批的最終消費者,況且電子商務不受時間、地域的限制,因此較難形成集中的、有規模的配送流量,由此造成配送任務複雜而瑣碎,成本居高不下。降低配送服務價格,就要解決電子商務公司與物流配送企業之間在配送服務價格之間的矛盾,需要雙方的共同努力。
一方面電子商務公司考慮配送成本,儘量將網上銷售的商品控制在與物流企業協議確定的配送範圍之內,並儘量使之相對集中且形成規模。
另一方面,物流配送企業應積極協作,選擇最短路徑作為配送路徑降低配送成本,並加強管理,開源節流,降低物流成本和配送服務的價格,同時還應儘可能與電子商務公司建立長期穩定的協作關係,這樣做有利於物流企業制定長遠投資和服務計劃,有利於加快新的物流配送技術的應用,加大配送渠道和設施的建設力度,最終有利於加快實現物流配送系統的信息化、自動化、網路化和智能化從長遠看,有利於持續穩定地降低物流配送的成本和價格。
目前關於物流配送的問題已經有很多方法,大致可分為定性和定量兩大類。定性方法是指憑藉個人或集體的經驗來做出決策,它的執行步驟一般是先根據經驗確定評價指標對各待選中心利用評價指標進行優劣性檢驗,根據檢驗結果作出決策。
定性方法的優點是註重歷史經驗、簡單易行,其缺點是容易犯經驗主義和主觀主義的錯誤,並且當可選地點較多時不易做出理想的決策。定量方法根據各種約束條件和所要達到的目標,把選址問題轉化為函數,再利用合適的演算法進行求解,求出最符合條件的解即具體的地點作為配送路徑。基於最短距離改進問題的演算法的物流配。
一、最短路徑法
採用圖論中的最短路徑演算法來建立物流配送路徑選擇模型。它的主要思想是從代表兩個頂點的距離的權矩陣開始,每次插人一個頂點比較任意兩點間的已知最短路徑和插人頂點作為中間頂點時可能產生的路徑距離,然後取較小值以得到新的距離權矩陣。當所有的頂點均作為頂點時,得到的最後的權矩陣就反映了所有頂點間的最短距離信息。最短距離者作為費用最小者,即最佳的選址位置。
由於最短路徑問題有著廣泛的應用背景,國內外大量專家學者都對此問題進行了深入的研究。經典的圖論與不斷完善的電腦數據結構及演算法的有效結合,使得新的最短路徑演算法不斷涌現。據統計,目前提出的此類最短路徑的演算法大約有種。而等人對其中的17種進行了測試,結果顯示有種效果比較好,它們分別是:TQQ(graph growthwith two queues)、DKA(the the Dijkstra'salgorithmimplemented with doubl ebuckets)。其中TQQ演算法的基礎是圖增長論,用兩個FIFO隊列實現了一個雙端隊列結構來支持搜索過程,較適合於計算單源點到其他所有點的最短距離。後兩種演算法則是基於Dijkstra演算法,採用桶結構明顯提高了永久標記點的搜索速度。
二、演算法原理及應用
演算法是由荷蘭電腦科學家艾茲格·迪科斯徹提出的,可用來找出圖中指定節點到其他節點間的最短距離。其主要思想是首先從源點求出長度最短的一條路徑,然後通過對路徑長度迭代得到從源點到其他各目標節點的最短路徑。具體求解過程如下:
設wj是從源點s到節點j的最短路徑長度pj是從s到的最短路徑中j點的前一節點。是標識集合。是未標識集合是節點集合。dij是節點i到節點j的距離(i與j直接相連,否則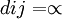 )。
)。
(1)S={s};T=M-S;wj=ds;(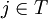 ,s與j直接相連)或
,s與j直接相連)或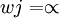
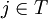 ,s與j不直接相連)。
,s與j不直接相連)。
(2)在T找節點i,使s到i的距離最小,並將i劃歸到S(可從與s直接相連的j中考慮)。若d_{ai}=mind_{aj}(i\inT),j與s直接相連,則將劃歸到中,即,,二修改中節點的值,若值改變,則。
(3)修改T中j節點的w_j值:wj = min(wj,wi + dij) 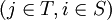 ;若wj值改變,則pj = i。
;若wj值改變,則pj = i。
(4)選定所有的wj最小值,並將其劃歸到S中這樣就得到一個與供應商、工廠及用戶間的最短距離,在費用、時間等方面的花費也相對要小得多,故可以將該物流中心選在該點處。
wi = minwj(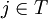 );
);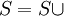 {i};T=T{i};若
{i};T=T{i};若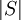 ,所有節點已標識,則演算法終止,否則,轉人步驟(3)。
,所有節點已標識,則演算法終止,否則,轉人步驟(3)。
Dijkstra演算法通用性強,既可以解決單源點間的最短路徑問題,也可解決所有點對之間的最短路徑問題,且編程簡單。將物流中心選在與所有點對距離最近的那個點即可。
三、路徑分析設計
實際生活中,城市道路網的表現形式一般為數字化的矢量地圖,其網路空間特征的交叉路口坐標和道路位置坐標藉助於地圖上的圖形來識別和解釋的。要對城市道路網運用Dijkstra演算法求解最短路徑,首先必須抽象城市道路網路為網路圖論中的網路圖,另外,系統要求計算道路上任意兩點間的最短路徑,而傳統Dijkstra演算法求解範圍局限於任意網路節點間,不能滿足要求,必須進行改進。
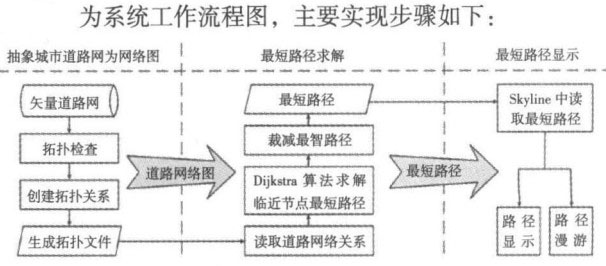
1.系統工作流程設計
隨著城市建設的加快,城市道路網路經常發生變化,為避免經常改寫代碼,增強程式的健壯性和提高最短路徑分析的運算效率,系統一般直接從拓撲文件提取道路網的網路拓撲結構並載入到記憶體中,一旦道路更新後,僅需重新抽象城市道路網路為網路圖並生成拓撲文件即可。
(1)抽象城市道路為網路圖。首先對城市道路進行編輯處理,使其與實際道路相符合,併進行拓撲檢查,生成線與線相互交叉的道路圖然後創建城市道路拓撲,拓撲關係構建了相鄰弧段和結點之間的關係最後生成道路網路拓撲文件,文件中定義了共屬性特征如弧段的起始節點、終止節點,弧段長度等,為最短路徑計算準備數據。
(2)最短路徑求解。首先讀取城市道路網路圖然後系統根據屏幕輸入坐標,尋找道路網中的最近點作為最短路徑分析的起點和終點,利用演算法計算滿足條件的弧段,並依順序連接所有弧段最後裁剪起終點兩端的多餘部分,返回最短路徑。
(3)最短路徑顯示與漫游。Skyline中通過程式介面讀取計算結果,併在三維場景中進行顯示和設定為路徑,系統提供模型角色沿路徑進行漫游瀏覽。演算法計算滿足條件的弧段,並依順序連接所有弧段最後裁剪起終點兩端的多餘部分,返回最短路徑。最短路徑顯示與漫游。中通過程式介面讀取計算結果,併在三維場景中進行顯示和設定為路徑,系統提供模型角色沿路徑進行漫游瀏覽。
2.數據存儲結構設計
ArcGIS是ESRI公司開發的一套完整的GIS應用產品,它通過對地理現象、事件及其關係進行可視化表達,構建特定的應用,提升工作效率。系統通過它進行城市道路的拓撲創建工作,並生成拓撲文件,把城市道路網抽象為關係圖。系統藉助ArcGIS的開發引擎ArcEngine快速訪問道路拓撲圖,並創建以下幾個類完成網路關係圖的存儲及最短路徑計算,如表所示。
四、路徑效果分析
隨著3S技術的飛速發展,“數字城市”成為更高層次的追求,人們越來越多地要求從三位空間處理問題。建立以配送為中心的物流服務體系。配送是商品市場發展的產物隨著大批量、少批次的物流配送活動逐步被小批量、多批次所取代,個性化、多樣化的市場需求越來越占有更多的市場份額,配送已成為電子商務時代物流活動的中心環節和最終目的。因此,一系列物流活動必須圍繞組織配送表現出活躍的市場機制。物流企業內部的所有部門和人員都應面向配送、面向市場、面向客戶。此外,物流企業要改變單一送貨的觀念,協助電子商務公司完成售後服務,提供更多的增值服務。內容,如跟蹤產品訂單、提供銷售統計和報表等。只有這樣才能緊跟電子商務的步伐,不被市場所淘汰。
物流配送時使用最短路徑分析的演算法設計。使得在配送時能夠選擇到配送點最短路徑,降低配送成本。通過多次實驗表明採用該演算法準確、可靠,為路徑分析在物流中的應用進一步擴展奠定了基礎。
- ↑ 凡金偉,呂康.基於Dijkstra演算法在物流配送中的應用[J].電腦編程技巧與維護,2009,(04)
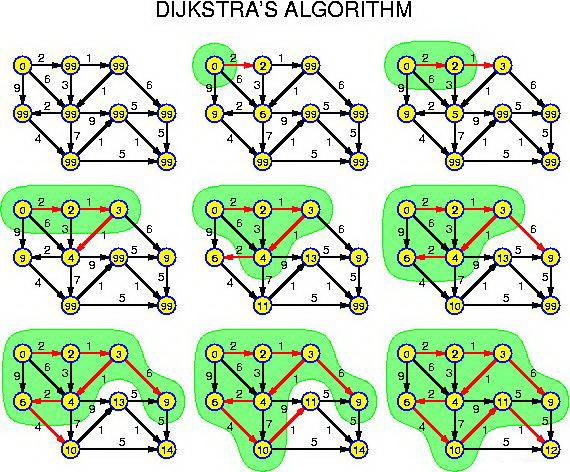









第6個圖和最後一個圖順序是不是反了