路徑分析
出自 MBA智库百科(https://wiki.mbalib.com/)
- 路徑分析(Path Analysis)
目錄 |
什麼是路徑分析[1]
路徑分析是一種找尋頻繁訪問路徑的方法,它通過對Web伺服器的日誌文件中客戶訪問站點訪問次數的分析,挖掘出頻繁訪問路徑。
路徑分析的核心[2]
路徑分析是GIS中最基本的功能,其核心是對最佳路徑和最短路徑的求解。
- ①最佳路徑
從網路模型的角度看,最佳路徑求解就是在指定網路的兩結點間,找一條阻礙強度最小的路徑。最佳路徑的產生基於網線和結點轉角(如果模型中結點具有轉角數據的話)的阻礙強度。
例如,如果要找最短的路徑,阻礙強度要預先設定為通過網線或在結點轉彎處所花費的時間;如果要找費用最小的路徑,阻礙強度就應該是費用。當網線在順逆兩個方向上的阻礙強度都是該網線的長度,而結點無轉角數據或轉角數據都是0時,最佳路徑就成為最短路徑。
在某些情況下,用戶可能要求系統能一次求出所有結點間的最佳路徑,或者要瞭解兩結點間的第二、第三乃至第X條最佳路徑。
- ②最佳遍歷方案
另一種路徑分析功能是最佳遍歷方案的求解。
網線最佳遍歷方案求解是給定一個網線集合和一個結點,求解最佳路徑,使之由指定結點出發至少經過每條網線一次而回到起始結點。
結點最佳遍歷方案求解則是給定一個起始結點、一個終止結點和若幹中間結點,求解最佳路徑,使之由起點出發遍歷全部中間結點而達到終點。
路徑分析的類型[3]
(1)靜態求最佳路徑:由用戶確定權值關係後,給定每條弧段的屬性,當求最佳路徑時,讀出路徑的相關屬性,求最佳路徑。
(2)N條最佳路徑分析:確定起點、終點,求代價較小的幾條路徑。在實際應用中僅求出最佳路徑並不能滿足要求,可能NN某種因素不走最佳路徑,而走近似最佳路徑。
(3)最短路徑:確定起點、終點和所要經過的中間連線,求最短路徑。
(4)動態最佳路徑分析:實際網路分析中權值是隨著權值關係式變化的,而且可能會臨時出現一些障礙點,所以往往需要動態地計算最佳路徑。
路徑分析的內容[4]
路徑分析包含了兩個基本內容:一個是路徑的搜索;另一個是距離的計算。路徑搜索的演算法與連通分析是一致的,通過鄰接關係的傳遞來實現路徑搜索。路徑的長度(距離)以積聚距離(accumulated distance)來計算。距離的計算方法為:將柵格路徑視做由一系列路徑段(path segments)組成,在進行路徑搜索的同時計算每個路徑段的長度並累計起來,表示從起點到當前柵格單元的距離。這裡路徑段指的是在一定的精度範圍內可以以直線段模擬和計算的柵格單元集合。
路徑分析的兩大類[4]
路徑分析包含兩大類:一是有預定軌跡網路的路徑分析;二是無預定軌跡的路徑分析。前者是比較常見的類型,例如交通網路中的最短路徑分析、次短路徑分析、最優路徑分析以及網路的最小生成樹分析等等,這類分析的特點是在空間中移動的對象只能沿著既定的路線移動;後者接近於錶面分析,在空間中移動的對象有全部或者部分的自由度,沒有明確的路徑限制,無預定路徑的路徑分析就是要在給定的自由度內尋找滿足特定條件的路徑,比如通過沼澤地的路徑選擇、有暗礁海域的航線規劃等等都屬於無預定軌跡情況下的路徑分析。
- 1.有預定軌跡的路徑分析
有預定軌跡的路徑分析主要包括最短路徑分析、最優路徑分析和最小生成樹分析等。其中,最短路徑分析是基礎。最短路徑演算法的主要設計思想是:以具有同樣拓撲結構和流限制屬性的虛擬網路系統代替研究對象,虛擬網路每個點都有可燃性,在起點點火,火勢沿網路路徑傳播,最先到達終點的火焰所經過的軌跡便是最短路徑。路徑點數據結構如下:
struct Path Point Class
{
TPoint tpThisPoint;//當前點的坐標
in liLastPosition;//本路徑前驅點的索引值
bool bExtFlag;//擴張標識
float fDistance;//本路徑當前的積聚距離
}
演算法表述如下:
(1)讀取流的屬性,根據約束集更新網路基本拓撲,對結點數組賦初值。
(2)掃描研究區域,找到起點S和終點C。
(3)記起點S的積聚路徑距離(以下簡稱距離)為0,並放人結點路徑距離數組Path DiStanCe。
(4)對S點以八鄰域方向按以下規則進行一次擴張:若相鄰像素v為黑色(未經搜索過的路徑),則將v點的坐標記人路徑距離數組,記v的前驅索引值為當前點在數組中的系列值,將v路徑距離記為當前點的積聚距離與v到當前點的距離之和,將v的擴張標識記為未擴張。若相鄰像素v為淺灰色(已經搜索過的路徑),則接著處理下一鄰域方向。當前點的八鄰域方向搜索完畢以後,對當前點加已擴張標識。
(5)對擴張得到的結點集合按其積聚距離進行處理:
①若最大積聚距離值與最小積聚距離值的差超過0.5,則按與最大積聚距離的差值以0.5為閡值進行分組,對差值大於0.5的結點按(4)中的規則進行一次擴張,將擴張結果集加人到差值小於0.5的結點集中。
②若最大積聚距離與最小積聚距離的差值小於0.5,則直接對擴張後得到的結點集進行新的擴張。
(6)重覆(5)直至遇到終點或結點路徑距離數組中沒有未擴張結點。
(7)考查終點的八鄰域像素,如果無綠色像素則轉①,否則轉②。
①起點與終點不連通,運算結束。
②找到最短路徑。記錄最短路徑距離值,路徑回溯方法為:從終點開始,根據數組中記錄的前驅關係回溯路徑,並標以標識色(深色)染路徑直至起點,結束運算。
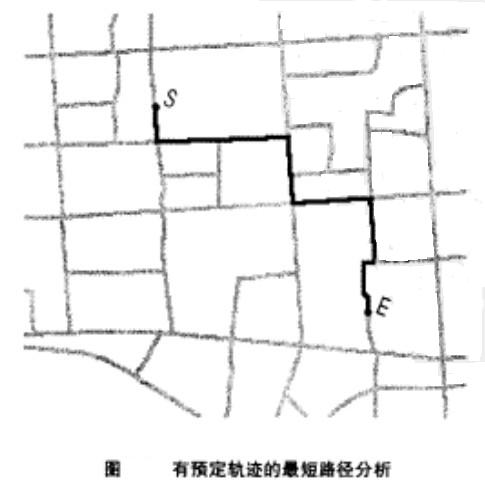
下圖是上述演算法的示例,其中深色的軌跡就是所得到的最短路徑。
通過以上演算法可以得到起點和終點數目都為1的最短路徑,計算起點到其他n - 1頂點地球信息理論和零初始化問題的最短路徑,只需繼續擴張直到結點數組中沒有未擴張結點,然後從其他n - 1個結點分別進行回溯,找到距起點的最短路徑。
全源最短路徑的演算法可以首先遍歷網路,記錄網路中相鄰兩結點間的距離,得到鄰接結點間的距離矩陣,然後採用Floyd方法計算所有點對之間的最短距離矩陣。
- 2.無預定軌跡的路徑分析
流在空間中流動時,並不一定有嚴格的既定線狀路徑限制,而具有全部或者部分的自由度。例加航空、航海的航線等、無預定軌跡的最短路徑分析,是有預定軌跡路徑分析的廣義問題,適用範圍更廣。對於具有全部自由度的流流動,可以抽象成平面上全連通網路的網路分析,所有結點之間都以直線連接,從而轉化為普通的圖論問題。無預定軌跡的路徑分析主要側重於障礙空間的路徑分析,此類分析在網路分析、機器人學、最優化方法以及計算幾何等領域中有重要的價值。