AK模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
AK模型假設不變的外生儲蓄率和固定的技術水平,可以解釋消除報酬遞減後將如何導致內生增長。
1. AK生產函數及其性質
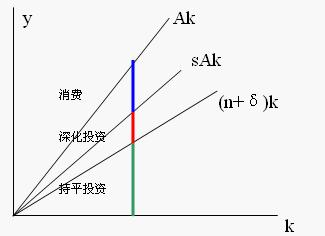
設新的生產函數為Y=AK,A為反映技術水平的常數,K為資本存量則人均產出為y=Ak,k為人均資本存量。圖示:
生產函數的性質:
- 規模收益不變:λY=A(λK) 。
- 資本的邊際產品 不變為常數。
2. 投入品的變動
(1)勞動力的增長: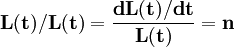
(2)知識的增長: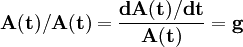 ,g為表示技術進步率的外生參數,由於假定技術為固定的常數,因此g=0;
,g為表示技術進步率的外生參數,由於假定技術為固定的常數,因此g=0;
(3)資本的增長: ,其中s為儲蓄率,δ為資本折舊率,均為外生變數;
,其中s為儲蓄率,δ為資本折舊率,均為外生變數;
3.增長路徑的動態
類似於索洛模型,有:
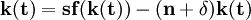
則,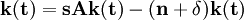
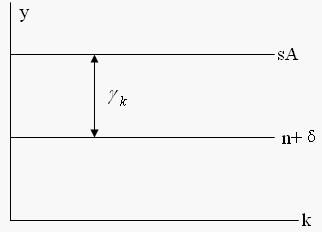
令k的增長率λk=k/k,則: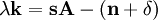
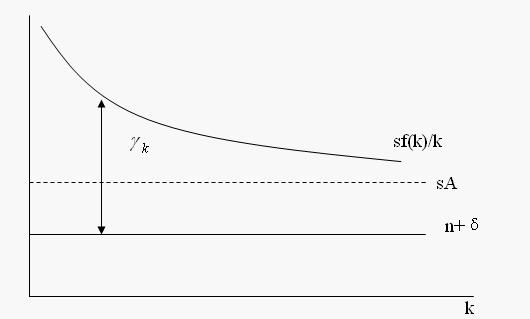
當sA > (n + δ)時,增長情況如下圖所示:
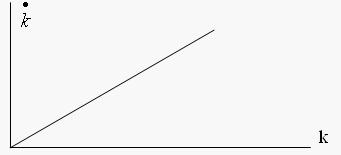
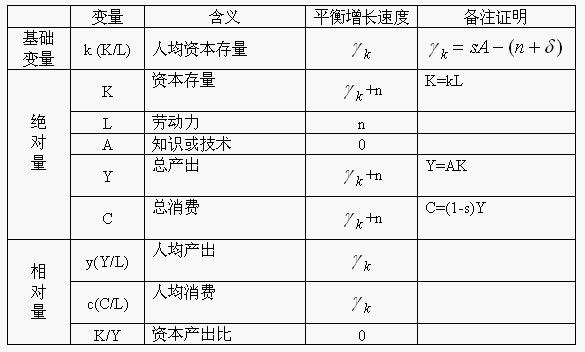
由於k以穩定的速度λk增長,k不會收斂於某一個穩態的值,因此k與其他變數的增長是發散的。各變數的增長路徑如下:
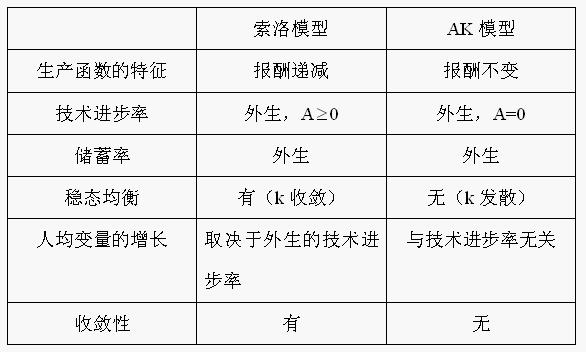
AK模型與索洛模型的比較
AK模型的一個擴展:資本報酬不變與收斂性並存
考慮生產函數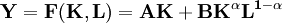 ,它是AK型生產函數與C-D型生產函數的混合,體現了報酬不變和報酬遞減的共同性質。其人均形式可寫為:
,它是AK型生產函數與C-D型生產函數的混合,體現了報酬不變和報酬遞減的共同性質。其人均形式可寫為:
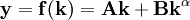
則k的增長率:
![\mathbf{\lambda k=\frac{sf(k)}{k}-(n+\delta)=s(A+k^{\alpha-1})-(n+\delta)=sk^{\alpha-1}+[sA-(n+\delta)]}](/w/images/math/1/9/d/19d580499b08db8c198e6b288b522c6a.png)
如果sA > n + δ,則增長動態為下圖所示:
AK模型揭示了放棄資本收益遞減規律如何能夠導致內生增長。不過,該模型存在明顯的缺陷:
1.該模型似乎過於簡單,直接放棄資本收益遞減規律似乎不符合人們的常識;
2.該模型不能預測絕對收斂或條件收斂,而條件收斂顯然是一條經驗規律。如果將k僅視為物質資本,那麼ak生產函數顯然不符合經驗規律。不過,如果將k理解為包括人力資本在內的廣義資本概念,該生產函數也還大致說得過去。
3.此外,ak模型直接放棄資本收益遞減規律似乎過於突兀,不過,內生增長模型(尤其是下文介紹的外部性模型)在很大程度上可以歸結為ak模型的形式:在這些模型中,雖然在個體水平上存在收益遞減,但由於外部性或溢出效應的存在,總量水平上則表現出不變收益或遞增收益。ak模型有助於我們理解這些更重要的模型。
至於ak模型對經驗規律即條件收斂的違反,我們可以對ak模型進行簡單的擴展,從而在保留資本收益不變特征的同時恢復模型的收斂性質。這正是多數凸性增長模型的實際做法。我們知道,新古典生產函數能夠產生收斂,ak生產函數則能夠產生內生增長,將二者結合在一起,我們就可以得到既具有內生增長又具有收斂性質的經濟增長模型。該生產函數具有資本收益遞減的性質(從而具有收斂性質),但資本邊際產品的遞減是有下界的(從而產生內生增長)。