高斯－馬爾可夫定理

出自 MBA智库百科(https://wiki.mbalib.com/)

高斯－馬爾可夫定理（Gauss-Markov Assumptions）

　　在統計學中，高斯－馬爾可夫定理是指在誤差零均值，同方差，且相關的線性回歸模型中，回歸繫數的最佳線性無偏估計就是最小方差估計。一般而言，任何回歸繫數的線性組合之BLUE（Best Linear Unbiased Estimators）就是它的最小方差估計。在這個線性回歸模型中，其誤差不需要假定為正態分佈或獨立同分佈（而僅需要滿足相關和方差這兩個稍弱的條件）。

　　指在給定經典線性回歸的假定下，最小二乘估計量是具有最小方差的線性無偏估計量的這一定理。

　　高斯--馬爾可夫定理的意義在於，當經典假定成立時，我們不需要再去尋找其它無偏估計量，沒有一個會優於普通最小二乘估計量。也就是說，如果存在一個好的線性無偏估計量，這個估計量的方差最多與普通最小二乘估計量的方差一樣小，不會小於普通最小二乘估計量的方差。

　　具體而言，假設

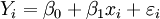　　。（i = 1……n）

　　其中β₀和β₁是非隨機且未觀測到的參數，x_i 是觀測到的變數，ε_i是隨機誤差，Y_i是隨機變數（x小寫:因x非為隨機變數，Y大寫:因Y為隨機變數）。

　　高斯－馬爾可夫定理的條件是：

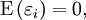
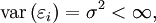
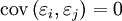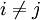　　，，也就是“不相關性”。

　　β_i的線性無偏估計指的是E{x'e}=0使得E{b}=β

  高斯－馬爾可夫定理是一個小作品。你可以通過編輯或修訂擴充其內容。