韋伯區位三角形

出自 MBA智库百科(https://wiki.mbalib.com/)

　　韋伯區位三角形是德國經濟學家韋伯在工業區位論中的關於工業區位選擇的幾何學分析模型。韋伯的“區位三角形”模型認為：運費與距離和重量相關，運費最小點(P) 為原料地 M1、原料地 M2 和市場 C 構成的區位三角形的重力中心，運費最小點(P) 即企業的最佳區位。

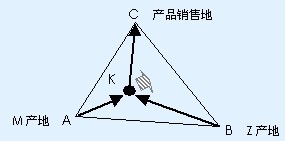
　　考慮兩種原材料區位性的情形。假設原材料M產地為A，原材料Z產地為B；產品的運費率為t1，原材料M的運費率為t2，原材料Z的運費率為t3；其他條件不變。企業現在要選擇的區位就是要以三項運費率決定的成本之和最小。這時企業的選址一定是在這三點圍成的三角形內部的某一點，設該點為K，此時運輸總成本

T = t₁S_B + t₂S_A + t₃S_C，達到最小。如圖所示。

　　假如原材料M的運費率t2降低，企業可以向B和C靠近(圖中的陰影箭頭方向)。因為企業到A的距離增加雖然增加了原材料M的運費，但會減少運輸Z和產品的成本，從而會降低企業的總運輸成本。因為M的運費率降低而節約的運輸成本大於增加的運輸成本。

　　工業區位論揭示了企業選址原理，運用這一原理研究城市中各種經濟主體的選址併進而依據這種選擇研究城市的區位原因及整體佈局規劃，都是非常方便的分析工具。故工業區位論是城市經濟學的基礎理論之一。

　　在西方工業區位學說史上，德國經濟學家龍哈德(W. Launhard) 和韋伯都先後運用幾何學分析方法構建工業區位選擇模型。龍哈德的“重量三角形”模型(即最小費用的區位模型) 認為 :兩點代表原材料來源地，一點代表產品銷售地，距三個頂點的直線交點而噸公裡數之和又是最小的位置即為最優區位 。此為工業區位論的最初論證和早期模型 。

　　韋伯的“區位三角形”模型認為運費與距離和重量相關，運費最小點(P) 為原料地 M1、原料地 M2 和市場 C 構成的區位三角形的重力中心，運費最小點(P) 即企業的最佳區位。任美鍔對韋伯“區位三角形”模型作瞭如下通俗化介紹“一種工業：品的生產，所需運輸的物資，不外原料、燃料和成品三種， ……工廠最適宜的位置自然是在三者間相對82運費最小的地點。運費的決定視貨物的重量與其必需運輸的距離而定， ……工廠的區位，不但須視其離原料產地、燃料產地、市場的距離，並且還要顧到原料、燃料和成品的重量。所以在決定工業區位的時候，原料、燃料和成品間的相對比重，視三者的距離和重量的乘積而定，這便是韋伯氏的重量三角形定理。根據這個定理，運費最小點(即設廠地點) 可以用數學的方法正確求得”。任氏的上述介紹揭示了韋伯“區位三角形”模型的基本內涵，並創造性地將“原料產地 M1”、“原料產地 M2”區分為“原料產地”、“燃料產地”。但也存在明顯的失誤，即將龍哈德倡導的“重量三角形”術語與韋伯倡導的“區位三角形”術語混用。

• 工業區位論