零增長模型
出自 MBA智库百科(https://wiki.mbalib.com/)
零增長模型(Zero Growth Model)
目錄 |
零增長模型是股息貼現模型的一種特殊形式,它假定股息是固定不變的。換言之,股息的增長率等於零。零增長模型不僅可以用於普通股的價值分析,而且適用於統一公債和優先股的價值分析。
零增長模型實際上也是不變增長模型的一個特例。特別是,假定增長率合等於零,股利將永遠按固定數量支付,這時,不變增長模型就是零增長模型。這兩種模型來看,雖然不變增長的假設比零增長的假設有較小的應用限制,但在許多情況下仍然被認為是不現實的。但是,不變增長模型卻是多元增長模型的基礎,因此這種模型極為重要。
零增長模型假定股利增長率等於0,即g=0,也就是說未來的股利按一個固定數量支付。貼現現金流模型的公式如下:
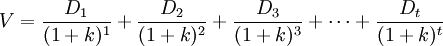 (1)
(1)
式中:
根據這個假定,我們用D0來改換方程(1)中的Dt:

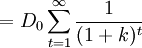 (2)
(2)
因為k>0,按照數學中無窮級數的性質,可知:

代入公式(2.21)中,得出零增長模型公式:
 (3)
(3)
式中:
- V——股票的內在價值;
- D0——在未來無限時期支付的每股股利;
- k——到期收益率。
例如,假定某公司在未來無限時期支付的每股股利為8元,必要收益率為10%,運用公式(3),可知1股該公司股票的價值等於8/0.10=80(元),而當時1股股票價格為65元,每股股票凈現值等於80-65=15(元),說明該股股票被低估15元,因此建議可以購買該種股票。
零增長模型的應用似乎受到相當的限制,畢竟假定對某一種股票永遠支付固定的股利是不合理的。但在特定的情況下,對於決定普通股票的價值,仍然是有用的。而在決定優先股的內在價值時,這種模型相當有用,因為大多數優先股支付的股利是固定的。








不錯