零增长模型
出自 MBA智库百科(https://wiki.mbalib.com/)
零增长模型(Zero Growth Model)
目录 |
零增长模型是股息贴现模型的一种特殊形式,它假定股息是固定不变的。换言之,股息的增长率等于零。零增长模型不仅可以用于普通股的价值分析,而且适用于统一公债和优先股的价值分析。
零增长模型实际上也是不变增长模型的一个特例。特别是,假定增长率合等于零,股利将永远按固定数量支付,这时,不变增长模型就是零增长模型。这两种模型来看,虽然不变增长的假设比零增长的假设有较小的应用限制,但在许多情况下仍然被认为是不现实的。但是,不变增长模型却是多元增长模型的基础,因此这种模型极为重要。
零增长模型假定股利增长率等于0,即g=0,也就是说未来的股利按一个固定数量支付。贴现现金流模型的公式如下:
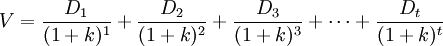 (1)
(1)
式中:
根据这个假定,我们用D0来改换方程(1)中的Dt:

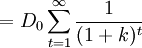 (2)
(2)
因为k>0,按照数学中无穷级数的性质,可知:

代入公式(2.21)中,得出零增长模型公式:
 (3)
(3)
式中:
- V——股票的内在价值;
- D0——在未来无限时期支付的每股股利;
- k——到期收益率。
例如,假定某公司在未来无限时期支付的每股股利为8元,必要收益率为10%,运用公式(3),可知1股该公司股票的价值等于8/0.10=80(元),而当时1股股票价格为65元,每股股票净现值等于80-65=15(元),说明该股股票被低估15元,因此建议可以购买该种股票。
零增长模型的应用似乎受到相当的限制,毕竟假定对某一种股票永远支付固定的股利是不合理的。但在特定的情况下,对于决定普通股票的价值,仍然是有用的。而在决定优先股的内在价值时,这种模型相当有用,因为大多数优先股支付的股利是固定的。








不错