阿蒂亞－辛格指標定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
在數學中，阿蒂亞-辛格指標定理是指：對於緊流形上的橢圓偏微分運算元，其解析指標（與解空間的維度相關）等於拓撲指標（決定於流形的拓撲性狀）。它涵攝了微分幾何中許多大定理，在理論物理學中亦有應用。
此定理由邁克爾•阿蒂亞與艾沙道爾•辛格於1963年證出。
X 是緊微分流形。
E 與 F 是 X 上的向量叢。
是向量叢之間的橢圓偏微分運算元。
設 D 是帶 k 個變元 
的 n 階微分運算元。其符號定義是以 
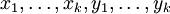為變元的函數，其定義是將
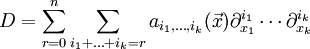
映至
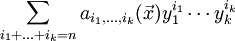
因此符號對變元 
是個 n 次齊次多項式。若此多項式滿足 
，則稱 D 是橢圓運算元。
例一：帶 k 個變元的拉普拉斯運算元其符號為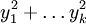 
，這是一個橢圓運算元。
以上所述是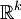 
上的偏微分運算元。今考慮微分流形 X，其上的 n 階偏微分運算元可以藉局部坐標系定義。此時其符號是 X 的餘切叢 
上的函數；對固定的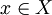 
，其符號是向量空間 
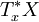上的 n 次齊次函數，此定義與局部坐標的選取無關（偏微分運算元在坐標變換下的變換較為複雜，只能以射流叢定義；然而其最高階項的變換規律似於張量）。
進一步言之，對於向量叢之間的偏微分運算元 
（一樣以局部坐標定義），其符號是拉回叢 pHom(E,F) 的截面。若對每個 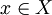，此符號限製為可逆映像 
，則稱 D 為橢圓運算元。
粗略來說，橢圓運算元的關鍵特性在於它們幾乎可逆。對於緊流形上的橢圓運算元 ，存在一個橢圓偽微分運算元 D' 使得 DD' 與 D'D 都是緊運算元。由此可推知 D 的核與餘核都是有限維的。
既然 D 有偽逆，它便是 Fredholm 運算元。對這類運算元，可定義指標為
Index(D) = Dim Ker(D) − Dim Coker(D) = Dim Ker(D) − Dim Ker(D)。
在微分幾何的脈絡下，常另稱為D的解析指標。
例二：考慮流形 
，運算元 
，其中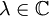 
，這是最簡單的橢圓運算元。若 
，則 
，反之則為零空間；其伴隨運算元 D * 滿足類似的性質，不難算出 D 的指數為零。由此例可見 
與 
在 λ 變化時可能有不連續點，但其差則是個常數。
設 X 是 n 維緊微分流形，橢圓偏微分運算元 的拓撲指標定義為
ch(D)Td(X)[X]
換言之，是同調類 ch(D)Td(X) 的最高維項在 X 的基本同調類上的取值。在此：
Td(X) 是流形的 Todd 類。
ch(D) = φ − 1(ch(d(pE,pF,σ(D)))，在此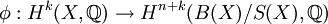 
是托姆同構，B(X),S(X) 指單位球叢及其邊界。
ch 是陳特征，σ(D) 是 D 的符號，而 d(pE,pF,σ(D)) 是 K 理論中定義的差元。
符號同前。橢圓運算元 D 的解析指標在微小的擾動下不變，因此產生了一個自然的問題，稱為指標問題：可否以流形 X 及向量叢 E,F 的拓撲不變數表示解析指標？
阿蒂亞-辛格指標定理給出的解答是：
D 的解析指標等於拓撲指標
解析指標通常難以計算，而拓撲指標儘管定義複雜，卻往往有直截了當的幾何意義。藉由選取適當的橢圓運算元 ，指標定理可以給出豐富的幾何信息。
蓋爾芳特首先註意到解析指標的同倫不變性，併在1959年提出了橢圓運算元的指標問題，希望以流形的拓撲不變數描述解析指標。黎曼-羅赫定理是最早知道的特例；另一方面，波萊爾與希策布魯赫早先證明瞭自旋流形的Â虧格的整性，並猜想這個性質可以由某個狄拉克運算元的指標詮釋。這個問題也由阿蒂亞與辛格在1961年連手解決。
阿蒂亞與辛格在1963年宣佈他們的指標定理，但一直沒有正式發表，只出現在 Palais 在1965年出版的書上。他們在1968年發表了第二個證明，用K理論取代了初版證明中的配邊論手法。
阿蒂亞、拉烏爾•博特與 Patodi 在 1973 年以熱傳導方程的手法給出另一個證明。格茨勒基於愛德華•維騰（1982）及 Alvarez-Gaume（1983）的想法，給出了局部狄拉克運算元的局部指標定理的簡短證明，這涵攝了實際應用中的大多數例子。
偽微分運算元的想法可以從歐氏空間上的常繫數偏微分運算元解釋，在此情況下，這些運算元不外是多項式函數的傅立葉變換；如果我們容許更一般的函數，其傅立葉變換就構成了偽微分運算元。對於一般的流形，可以透過局部坐標系定義偽微分運算元，只是手續稍微繁瑣一些。
指標定理的許多證明中都利用偽微分運算元，而非一般的微分運算元，因為前者的理論更富彈性。舉例來說，橢圓運算元的偽逆不是微分運算元，卻仍是偽微分運算元；另一方面，群 K(B(X),S(X)) 的元素對應到橢圓偽微分運算元的符號。
對偽微分運算元可以定義階數，這個數可以是任意實數，甚至是負無窮大；此外也能定義其符號。橢圓偽微分運算元定義為對長度夠長的餘切向量為可逆的偽微分運算元。指標定理的多數版本皆可推廣到橢圓偽微分運算元的情形。
指標定理的首個證明奠基於希策布魯赫-黎曼-羅赫定理，並運用到配邊理論與偽微分運算元。想法簡述如下。
考慮由資料 (X,V) 構成的環，其中 X 是緊定向微分流形，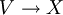
是向量叢，其加法與乘法分別由不交並與積導出；我們考慮此環對關係 
的商環。這個構造類似於配邊環，不過此時我們還慮及流形上的向量叢。解析指標與拓撲指標皆可詮釋為從此環映至整數環的同態。托姆的配邊理論給出了這個環的一組生成元，我們可以對這些較簡單的例子驗證指標定理，從而導出一般的情形。
阿蒂亞與辛格正式發表的第一個證明採用了K理論。設 X,Y 為緊流形，
為閉浸入，他們對橢圓運算元定義了一個推前運算 i!，並證明 i! 保持指標。我們一方面可取 Y 為一個包括 X 的高維球面；另一方面，仍取 Y 為前述球面，而 X 為其內一點。由於 i! 保持指標，而拓撲指標也具備兼容的運算，兩相比較後可將指標定理化約到一個點的情形，此時極易證明。
阿蒂亞、博特 與 Patodi 在1973年給出了熱傳導方程手法的證明。格茨勒、伯利納與弗尼在2002年給出一個精神相近的簡化證明，其中利用了超對稱的想法。
設 D 為偏微分運算元，D * 為其伴隨運算元，則 D * D、DD * 是自伴運算元，並具有相同的非零特征值（記入重數），但是它們核空間不一定有相同維度。D 的指標寫作
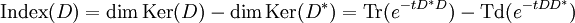
在此 t > 0 可任取。
上式右側是兩個熱核的差，它們在 
時有漸近表示式，它乍看複雜，但不變數理論表明其中有許多相銷項，藉此可明確寫下領導項，由此可證出指標定理。這些相銷現象稍後也得到超對稱理論的詮釋。
推廣至橢圓偽微分運算元的情形。
考慮更一般的橢圓復形，這是一個由向量叢構成的上鏈復形
0 → E0 → E1 →E2 → ... → Em →0
其中的每個箭頭都是偽微分運算元，其符號構成一個正合復形。當只有兩項非零時，前述條件等價於其間的運算元是橢圓的，因此橢圓運算元是橢圓復形的特例。反過來說，給定一個橢圓復形，分別考慮其奇次項與偶次項的直和，其間的映射由原復形的映射及伴隨映射給出，如此則可得到橢圓運算元。
帶邊界的流形。
考慮一族以流形 Y 為參數空間而變化橢圓運算元，相應的解析指數可定義為 K(Y) 的元素。
設李群 G 作用在緊流形 X 上，並與所論的橢圓運算元交換，則我們可以用等變K理論替代一般的K理論，得到的結果稱為等變指標定里。
L2 指標定理。
設 X 為有定向的緊流形。任選一黎曼度量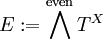，取 
，並取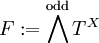 
，定義運算元 
。此時的拓撲指標等於 X 的歐拉示性數，解析指標等於 
。
設 X 為緊復流形，V 為其上的復向量叢。定義
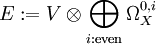
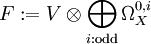
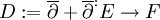
則解析指標等於
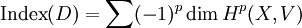
而拓撲指標等於
index(D) = ch(V)Td(X)[X],
流形的Â虧格是個有理數。對於自旋流形，這個值總是整數，若 
，則它還是個偶數。這個定理可以由指標定理導出，方法是考慮適當的狄拉克運算元；當 時，此運算元的核與餘核帶有四元數環上的向量空間結構，其復維度必為偶數，因此解析指標也必然是偶數。
當阿蒂亞與辛格在2004年獲得阿貝爾獎時，公告上是這麼形容阿蒂亞-辛格指標定理的：
科學家以隨時空改變的力與測量量描述世界。自然律以這些量的變化率表示，稱為微分方程。這些方程可以有個指標，這是方程的解數減去對所求值的限制數目。阿蒂亞-辛格指標以空間的幾何性質描述這個量。
