阿蒂亚-辛格指标定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
在数学中,阿蒂亚-辛格指标定理是指:对于紧流形上的椭圆偏微分算子,其解析指标(与解空间的维度相关)等于拓扑指标(决定于流形的拓扑性状)。它涵摄了微分几何中许多大定理,在理论物理学中亦有应用。
此定理由迈克尔•阿蒂亚与艾沙道尔•辛格于1963年证出。
X 是紧微分流形。
E 与 F 是 X 上的向量丛。
 是向量丛之间的椭圆偏微分算子。
是向量丛之间的椭圆偏微分算子。
设 D 是带 k 个变元  的 n 阶微分算子。其符号定义是以
的 n 阶微分算子。其符号定义是以 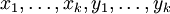 为变元的函数,其定义是将
为变元的函数,其定义是将
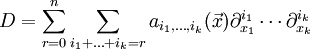
映至
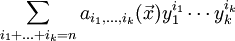
因此符号对变元  是个 n 次齐次多项式。若此多项式满足
是个 n 次齐次多项式。若此多项式满足 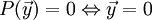 ,则称 D 是椭圆算子。
,则称 D 是椭圆算子。
例一:带 k 个变元的拉普拉斯算子其符号为 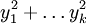 ,这是一个椭圆算子。
,这是一个椭圆算子。
以上所述是 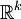 上的偏微分算子。今考虑微分流形 X,其上的 n 阶偏微分算子可以藉局部坐标系定义。此时其符号是 X 的余切丛
上的偏微分算子。今考虑微分流形 X,其上的 n 阶偏微分算子可以藉局部坐标系定义。此时其符号是 X 的余切丛  上的函数;对固定的
上的函数;对固定的 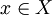 ,其符号是向量空间
,其符号是向量空间 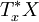 上的 n 次齐次函数,此定义与局部坐标的选取无关(偏微分算子在坐标变换下的变换较为复杂,只能以射流丛定义;然而其最高阶项的变换规律似于张量)。
上的 n 次齐次函数,此定义与局部坐标的选取无关(偏微分算子在坐标变换下的变换较为复杂,只能以射流丛定义;然而其最高阶项的变换规律似于张量)。
进一步言之,对于向量丛之间的偏微分算子  (一样以局部坐标定义),其符号是拉回丛 pHom(E,F) 的截面。若对每个
(一样以局部坐标定义),其符号是拉回丛 pHom(E,F) 的截面。若对每个 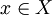 ,此符号限制为可逆映像
,此符号限制为可逆映像  ,则称 D 为椭圆算子。
,则称 D 为椭圆算子。
粗略来说,椭圆算子的关键特性在于它们几乎可逆。对于紧流形上的椭圆算子  ,存在一个椭圆伪微分算子 D' 使得 DD' 与 D'D 都是紧算子。由此可推知 D 的核与余核都是有限维的。
,存在一个椭圆伪微分算子 D' 使得 DD' 与 D'D 都是紧算子。由此可推知 D 的核与余核都是有限维的。
既然 D 有伪逆,它便是 Fredholm 算子。对这类算子,可定义指标为
Index(D) = Dim Ker(D) − Dim Coker(D) = Dim Ker(D) − Dim Ker(D)。
在微分几何的脉络下,常另称为D的解析指标。
例二:考虑流形  ,算子
,算子  ,其中
,其中 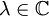 ,这是最简单的椭圆算子。若
,这是最简单的椭圆算子。若  ,则
,则  ,反之则为零空间;其伴随算子 D * 满足类似的性质,不难算出 D 的指数为零。由此例可见
,反之则为零空间;其伴随算子 D * 满足类似的性质,不难算出 D 的指数为零。由此例可见  与
与  在 λ 变化时可能有不连续点,但其差则是个常数。
在 λ 变化时可能有不连续点,但其差则是个常数。
设 X 是 n 维紧微分流形,椭圆偏微分算子  的拓扑指标定义为
的拓扑指标定义为
ch(D)Td(X)[X]
换言之,是同调类 ch(D)Td(X) 的最高维项在 X 的基本同调类上的取值。在此:
Td(X) 是流形的 Todd 类。
ch(D) = φ − 1(ch(d(pE,pF,σ(D))),在此 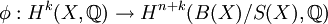 是托姆同构,B(X),S(X) 指单位球丛及其边界。
是托姆同构,B(X),S(X) 指单位球丛及其边界。
ch 是陈特征,σ(D) 是 D 的符号,而 d(pE,pF,σ(D)) 是 K 理论中定义的差元。
符号同前。椭圆算子 D 的解析指标在微小的扰动下不变,因此产生了一个自然的问题,称为指标问题:可否以流形 X 及向量丛 E,F 的拓扑不变量表示解析指标?
阿蒂亚-辛格指标定理给出的解答是:
D 的解析指标等于拓扑指标
解析指标通常难以计算,而拓扑指标尽管定义复杂,却往往有直截了当的几何意义。藉由选取适当的椭圆算子  ,指标定理可以给出丰富的几何信息。
,指标定理可以给出丰富的几何信息。
盖尔芳特首先注意到解析指标的同伦不变性,并在1959年提出了椭圆算子的指标问题,希望以流形的拓扑不变量描述解析指标。黎曼-罗赫定理是最早知道的特例;另一方面,波莱尔与希策布鲁赫早先证明了自旋流形的Â亏格的整性,并猜想这个性质可以由某个狄拉克算子的指标诠释。这个问题也由阿蒂亚与辛格在1961年连手解决。
阿蒂亚与辛格在1963年宣布他们的指标定理,但一直没有正式发表,只出现在 Palais 在1965年出版的书上。他们在1968年发表了第二个证明,用K理论取代了初版证明中的配边论手法。
阿蒂亚、拉乌尔•博特与 Patodi 在 1973 年以热传导方程的手法给出另一个证明。格茨勒基于爱德华•维腾(1982)及 Alvarez-Gaume(1983)的想法,给出了局部狄拉克算子的局部指标定理的简短证明,这涵摄了实际应用中的大多数例子。
伪微分算子的想法可以从欧氏空间上的常系数偏微分算子解释,在此情况下,这些算子不外是多项式函数的傅立叶变换;如果我们容许更一般的函数,其傅立叶变换就构成了伪微分算子。对于一般的流形,可以透过局部坐标系定义伪微分算子,只是手续稍微繁琐一些。
指标定理的许多证明中都利用伪微分算子,而非一般的微分算子,因为前者的理论更富弹性。举例来说,椭圆算子的伪逆不是微分算子,却仍是伪微分算子;另一方面,群 K(B(X),S(X)) 的元素对应到椭圆伪微分算子的符号。
对伪微分算子可以定义阶数,这个数可以是任意实数,甚至是负无穷大;此外也能定义其符号。椭圆伪微分算子定义为对长度够长的余切向量为可逆的伪微分算子。指标定理的多数版本皆可推广到椭圆伪微分算子的情形。
指标定理的首个证明奠基于希策布鲁赫-黎曼-罗赫定理,并运用到配边理论与伪微分算子。想法简述如下。
考虑由资料 (X,V) 构成的环,其中 X 是紧定向微分流形,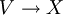 是向量丛,其加法与乘法分别由不交并与积导出;我们考虑此环对关系
是向量丛,其加法与乘法分别由不交并与积导出;我们考虑此环对关系  的商环。这个构造类似于配边环,不过此时我们还虑及流形上的向量丛。解析指标与拓扑指标皆可诠释为从此环映至整数环的同态。托姆的配边理论给出了这个环的一组生成元,我们可以对这些较简单的例子验证指标定理,从而导出一般的情形。
的商环。这个构造类似于配边环,不过此时我们还虑及流形上的向量丛。解析指标与拓扑指标皆可诠释为从此环映至整数环的同态。托姆的配边理论给出了这个环的一组生成元,我们可以对这些较简单的例子验证指标定理,从而导出一般的情形。
阿蒂亚与辛格正式发表的第一个证明采用了K理论。设 X,Y 为紧流形, 为闭浸入,他们对椭圆算子定义了一个推前运算 i!,并证明 i! 保持指标。我们一方面可取 Y 为一个包括 X 的高维球面;另一方面,仍取 Y 为前述球面,而 X 为其内一点。由于 i! 保持指标,而拓扑指标也具备兼容的运算,两相比较后可将指标定理化约到一个点的情形,此时极易证明。
为闭浸入,他们对椭圆算子定义了一个推前运算 i!,并证明 i! 保持指标。我们一方面可取 Y 为一个包括 X 的高维球面;另一方面,仍取 Y 为前述球面,而 X 为其内一点。由于 i! 保持指标,而拓扑指标也具备兼容的运算,两相比较后可将指标定理化约到一个点的情形,此时极易证明。
阿蒂亚、博特 与 Patodi 在1973年给出了热传导方程手法的证明。格茨勒、伯利纳与弗尼在2002年给出一个精神相近的简化证明,其中利用了超对称的想法。
设 D 为偏微分算子,D * 为其伴随算子,则 D * D、DD * 是自伴算子,并具有相同的非零特征值(记入重数),但是它们核空间不一定有相同维度。D 的指标写作
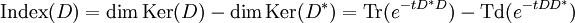
在此 t > 0 可任取。
上式右侧是两个热核的差,它们在  时有渐近表示式,它乍看复杂,但不变量理论表明其中有许多相销项,藉此可明确写下领导项,由此可证出指标定理。这些相销现象稍后也得到超对称理论的诠释。
时有渐近表示式,它乍看复杂,但不变量理论表明其中有许多相销项,藉此可明确写下领导项,由此可证出指标定理。这些相销现象稍后也得到超对称理论的诠释。
推广至椭圆伪微分算子的情形。
考虑更一般的椭圆复形,这是一个由向量丛构成的上链复形
0 → E0 → E1 →E2 → ... → Em →0
其中的每个箭头都是伪微分算子,其符号构成一个正合复形。当只有两项非零时,前述条件等价于其间的算子是椭圆的,因此椭圆算子是椭圆复形的特例。反过来说,给定一个椭圆复形,分别考虑其奇次项与偶次项的直和,其间的映射由原复形的映射及伴随映射给出,如此则可得到椭圆算子。
带边界的流形。
考虑一族以流形 Y 为参数空间而变化椭圆算子,相应的解析指数可定义为 K(Y) 的元素。
设李群 G 作用在紧流形 X 上,并与所论的椭圆算子交换,则我们可以用等变K理论替代一般的K理论,得到的结果称为等变指标定里。
L2 指标定理。
设 X 为有定向的紧流形。任选一黎曼度量,取 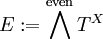 ,并取
,并取 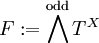 ,定义算子
,定义算子  。此时的拓扑指标等于 X 的欧拉示性数,解析指标等于
。此时的拓扑指标等于 X 的欧拉示性数,解析指标等于  。
。
设 X 为紧复流形,V 为其上的复向量丛。定义
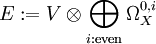
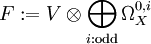
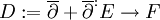
则解析指标等于
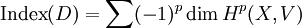
而拓扑指标等于
index(D) = ch(V)Td(X)[X],
流形的Â亏格是个有理数。对于自旋流形,这个值总是整数,若  ,则它还是个偶数。这个定理可以由指标定理导出,方法是考虑适当的狄拉克算子;当
,则它还是个偶数。这个定理可以由指标定理导出,方法是考虑适当的狄拉克算子;当  时,此算子的核与余核带有四元数环上的向量空间结构,其复维度必为偶数,因此解析指标也必然是偶数。
时,此算子的核与余核带有四元数环上的向量空间结构,其复维度必为偶数,因此解析指标也必然是偶数。
当阿蒂亚与辛格在2004年获得阿贝尔奖时,公告上是这么形容阿蒂亚-辛格指标定理的:
科学家以随时空改变的力与测量量描述世界。自然律以这些量的变化率表示,称为微分方程。这些方程可以有个指标,这是方程的解数减去对所求值的限制数目。阿蒂亚-辛格指标以空间的几何性质描述这个量。







