費雪方程式
出自 MBA智库百科(https://wiki.mbalib.com/)
費雪方程式(Fisher Equation)
目錄[隱藏] |
費雪方程式概述[1]
1.費雪方程式是表示國民收入水平與價格水平、貨幣供應量之間的數量關係的。利率有實際利率和名義利率之分。名義利率,是指沒有考慮通貨膨脹因素,按照承諾的貨幣價值計算的利率。實際利率,是對名義利率按貨幣購買力的變動修正後的利率。由於借貸雙方更關心貨幣的實際購買力而不是貨幣的名義額,因此實際利率能更準確地衡量借貸的成本和收益。名義利率的計價單位是貨幣,實際利率的計價單位則為標準化的一籃子商品和服務。若年名義利率為i,則現在投資1元,1年後將獲得1+i 元,若當年通貨膨脹率的預期值為π,按照現在的實際購買力計算,1年後的1+i 元只相當於現在的(1+i)/(1+π)。如果實際利率用R來表示,則應該具有下列關係:
1+R=(1+i)/(1+π)
由上述公式可以推導出:
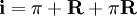
在通貨膨脹不是很嚴重的情況下,如預期的通貨膨脹率低於5%,最後一項πR的數值就非常小,可以忽略不計。因此上述關係式可以進一步簡化為:
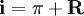
這就是著名的費雪方程式(Fisher Equation),該方程式是由美國偉大的經濟學家費雪提出的。費雪方程式表明,名義利率必須包含一個通貨膨脹溢價,以彌補預期的通貨膨脹給貸款人造成的實際購買力損失。當實際利率保持穩定時,名義利率就會隨著預期通貨膨脹率的提高而提高。
2.費雪方程式:是傳統貨幣數量論的方程式之一。20 世紀初 , 美國經濟學家歐文·費雪在《貨幣的購買力》一書中提出了交易方程式 , 也被稱為費雪方程式。
費雪效應可概括為:一國的名義利率反映了依該國預期的通貨膨脹調整後的真實回報率,也就是說造成各國名義回報率不同的原因,僅僅是因為通貨膨脹率的預期不同。在投資者可進行自由的國際投資的情況下,各地的預期真實回報趨於相等。如果出現了不相等的情況,投資者為追求較高的投資收益就會進行套利活動,而套利的結果又使各地的投資收益率趨於一致。
這一方程式為 :
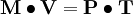
根據這一方程式 ,P 的值取決於 M,V,T3 個變數。費雪分析 , 在這3個經濟變數中
- M 是一個由模型之外的因素所決定的外生變數 ;
- V 是由制度因素決定的 , 而制度因素變化緩慢 , 因而可視為常數 ;
- T 與產出水平保持一定的比例 , 也是大體穩定的。
因此 , 只有 P和M的關係最重要 , 所以P的值特別是取決於M數量的變化。
交易方程式雖然主要說明 M 決定 P, 但當把 P 視為既定的價格水平時 , 則 :
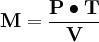
這說明 , 在既定的價格水平下 , 總交易量與所需要的名義貨幣量具有一定的比例關係 , 這個比例就是 1/V 。換言之,要使價格保持既定水平 , 只有當貨幣量與總交易量保持一定比例關係才能實現。
劍橋方程式與費雪方程式兩者在形式上基本相同,但二者在研究方法上、內容上卻有本質的區別;
(1) 對貨幣需求分析的側重點不同。費雪方程式強調貨幣的交易手段職能,側重於商品交易量對貨幣的需求;劍橋方程式強調貨幣作為一種資產的職能,側重於收入y的需求。
(2) 費雪方程式側重於貨幣流量分析,劍橋方程式側重於貨幣存量分析;
(3) 兩個方程式對貨幣需求的分析角度和所強調的決定貨幣需求因素有所不同。費雪方程式是對貨幣需求的巨集觀分析,劍橋方程式是從微觀角度對貨幣需求進行分析。
馬歇爾和庇古不僅僅將交易水平和影響人們交易方式的制度作為研究人們持有貨幣的關鍵要素,還探討了貨幣作為財富的一種被人們選擇所持有的原因和對貨幣需求量的影響。既然貨幣被人們選擇所持有,就不能排除利率的影響。但總體來說,劍橋方程式和費雪方程式差異很小,體現了貨幣中性論,即經濟中的實物經濟和貨幣經濟的“古典兩分法”思想。

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 













費雪方程式有兩條,另外一條是名義利率等於實際利率加上預期通貨膨脹率。而且一般情況下只叫這個為費雪方程式,上面的一般叫做交易方程式。望補充上去。