質數
出自 MBA智库百科(https://wiki.mbalib.com/)
質數(prime number)
目錄 |
質數又稱素數,有無限個。一個大於1的自然數,除了1和它本身外,不能被其他自然數(質數)整除,換句話說就是該數除了1和它本身以外不再有其他的因數;否則稱為合數。
根據算術基本定理,每一個比1大的整數,要麼本身是一個質數,要麼可以寫成一系列質數的乘積;而且如果不考慮這些質數在乘積中的順序,那麼寫出來的形式是唯一的。最小的質數是2。
目前為止,人們未找到一個公式可求出所有質數。
質數的個數是無窮的。歐幾裡得的《幾何原本》中有一個經典的證明。它使用了證明常用的方法:反證法。具體證明如下:假設質數只有有限的n個,從小到大依次排列為p1,p2,……,pn,設N=p1×p2×……×pn,那麼,N+1是素數或者不是素數。
如果N+1為素數,則N+1要大於p1,p2,……,pn,所以它不在那些假設的素數集合中。
如果N+1為合數,因為任何一個合數都可以分解為幾個素數的積;而N和N+1的最大公約數是1,所以N+1不可能被p1,p2,……,pn整除,所以該合數分解得到的素因數肯定不在假設的素數集合中。
因此無論該數是素數還是合數,都意味著在假設的有限個素數之外還存在著其他素數。所以原先的假設不成立。也就是說,素數有無窮多個。
其他數學家給出了一些不同的證明。歐拉利用黎曼函數證明瞭全部素數的倒數之和是發散的,恩斯特·庫默的證明更為簡潔,HillelFurstenberg則用拓撲學加以證明。
質數具有許多獨特的性質:
(1)質數p的約數只有兩個:1和p。
(2)初等數學基本定理:任一大於1的自然數,要麼本身是質數,要麼可以分解為幾個質數之積,且這種分解是唯一的。
(3)質數的個數是無限的。
(4)質數的個數公式π(n) 是不減函數。
(5)若n為正整數,在n2到(n + 1)2之間至少有一個質數。
(6)若n為大於或等於2的正整數,在n到n!之間至少有一個質數。
(7)若質數p為不超過n(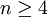 )的最大質數,則
)的最大質數,則 。
。
1.在一個大於1的數a和它的2倍之間(即區間(a, 2a]中)必存在至少一個素數。
2.存在任意長度的素數等差數列。(格林和陶哲軒,2004年[1] )
3.一個偶數可以寫成兩個質數之和,其中每一個數字都最多只有9個質因數。(挪威數學家布朗,1920年)
4.一個偶數必定可以寫成一個質數加上一個合成數,其中的因數個數有上界。(瑞尼,1948年)
5.一個偶數必定可以寫成一個質數加上一個最多由5個因數所組成的合成數。後來,有人簡稱這結果為 (1 + 5) (中國潘承洞,1968年)
6.一個充分大偶數必定可以寫成一個素數加上一個最多由2個質因數所組成的合成數。簡稱為 (1 + 2) (中國陳景潤)
質數被利用在密碼學上,所謂的公鑰就是將想要傳遞的信息在編碼時加入質數,編碼之後傳送給收信人,任何人收到此信息後,若沒有此收信人所擁有的密鑰,則解密的過程中(實為尋找素數的過程),將會因為找質數的過程(分解質因數)過久,使即使取得信息也會無意義。
在汽車變速箱齒輪的設計上,相鄰的兩個大小齒輪齒數最好設計成質數,以增加兩齒輪內兩個相同的齒相遇嚙合次數的最小公倍數,可增強耐用度減少故障。
在害蟲的生物生長周期與殺蟲劑使用之間的關係上,殺蟲劑的質數次數的使用也得到了證明。實驗表明,質數次數地使用殺蟲劑是最合理的:都是使用在害蟲繁殖的高潮期,而且害蟲很難產生抗藥性。
以質數形式無規律變化的導彈和魚雷可以使敵人不易攔截。
多數生物的生命周期也是質數(單位為年),這樣可以最大程度地減少碰見天敵的機會。







