網路分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
網路分析法（Analytic Network Process，ANP）
目錄 |
什麼是網路分析法[1]
網路分析法（ANP）是美國匹茲堡大學的T.L.Saaty教授於1996年提出的一種適應非獨立的遞階層次結構的決策方法，它是在層次分析法(Analytic Hierarchy Process,簡稱AHP)的基礎上發展而形成的一種新的實用決策方法。
AHP作為一種決策過程，它提供了一種表示決策因素測度的基本方法。這種方法採用相對標度的形式，並充分利用了人的經驗和判斷力。在遞階層次結構下，它根據所規定的相對標度—比例標度，依靠決策者的判斷，對同一層次有關元素的相對重要性進行兩兩比較，並按層次從上到下合成方案對於決策目標的測度。這種遞階層次結構雖然給處理系統問題帶來了方便，同時也限制了它在複雜決策問題中的應用。在許多實際問題中，各層次內部元素往往是依賴的C低層元素對高層元素亦有支配作用，即存在反饋。此時系統的結構更類似於網路結構。網路分析法正是適應這種需要，由AHP延伸發展得到的系統決策方法。
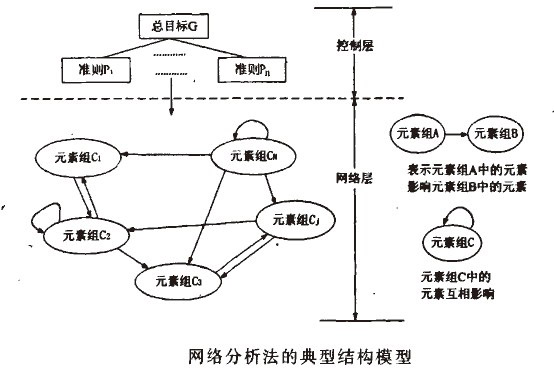
ANP首先將系統元素劃分為兩大部分：第一部分稱為控制因素層，包括問題目標及決策準則。所有的決策準則均被認為是彼此獨立的，且只受目標元素支配。控制因素中可以沒有決策準則，但至少有一個目標。控制層中每個準則的權重均可用AHP方法獲得。第二部分為網路層，它是由所有受控制層支配的元素組組成的C其內部是互相影響的網路結構，它是由所有受控制層支配的元素組成的，元素之間互相依存、互相支配，元素和層次間內部不獨立，遞階層次結構中的每個準則支配的不是一個簡單的內部獨立的元素，而是一個互相依存，反饋的網路結構。控制層和網路層組成為典型ANP層次結構，見下圖。
網路分析法的特點[2]
AHP通過分析影響目標的一系列因素，比較其相對重要性，最後選出得分最高的方案即為最優方案。Harker和Vargas曾經這樣評價AHP：“AHP是一套複雜的評價系統，當我們進行多目標、多準則以及多評委的決策時，面對眾多的可選方案，AHP能夠用來解決各種量化和非量化、理性與非理性的決策問題。”AHP簡單易用，其縝密的理論基礎決定了它能解決各種實際問題。AHP模型使各決策層之間相互聯繫，並能推出跨層次之間的相互關係。模型的頂層為企業的總目標，然後逐層分解成各項具體的準則、子準則等，直到管理者能夠量化各子準則的相對權重為止。
層次分析法能夠為決策者解決各種複雜系統問題，但它也存在一些缺憾。例如，AHP就未能考慮到不同決策層或同一層次之間的相互影響，AHP模型只是強調各決策層之間的單向層次關係，即下一層對上一層的影響。但在實際工作中對總目標層進行逐層分解時，時常會遇到各因素交叉作用的情況。如一個項目的不同研究階段對各評委的權重是不同的；同樣，各評委在項目研究的不同階段對各評價指標的打分也會發生變化。這時，AHP模型就顯得有些無能為力了。
網路分析法的特點就是，在層次分析法的基礎上，考慮到了各因素或相鄰層次之間的相互影響，利用“超矩陣”對各相互作用並影響的因素進行綜合分析得出其混合權重。而ANP模型並不要求像AHP模型那樣有嚴格的層次關係，各決策層或相同層次之間都存在相互作用，用雙箭頭表示層次間的相互作用關係。若是同一層中的相互作用就用雙迴圈箭頭表示。箭頭所指向的因素影響著箭尾的決策因素。基於這一特點，ANP越來越受到決策者的親睞，成為企業在對許多複雜問題進行決策的有效工具。ANP中各因素的相對重要性指標的確定與AHP基本相同。各因素的相對重要性指標（標度）是通過對決策者進行問卷調查得到的，但有時也會出現一些不一致的現象（如I與H比，標度為3；J與K比，標度為5；而I與K比，標度為6）。
網路分析法的案例分析[3]
- 案例：基於ANP的水電工程風險分析模型
- 1.水電工程風險因素識別
由於水電工程項目各分項工程眾多，且工程建設期一般較長，各分項工程面臨的風險也將多種多樣，對水電工程風險從總體上進行風險識別將有一定的難度，並且很可能遺漏較重要的風險因素，因此在識別風險前有必要將整體工程進行適當分項工程劃分，然後再對各分項工程進行風險識別。同時由於風險因素的多樣化，有必要也將風險按照一定的風險原則進行分解。因此本文采用項目分解結構(WBS)與風險分解結構(RBS)相結合的方法進行風險的識別。另外採用此方法進行風險識別也將有利於風險因素ANP結構模型的建立與求解。
- 2.工程項目的層次結構模型
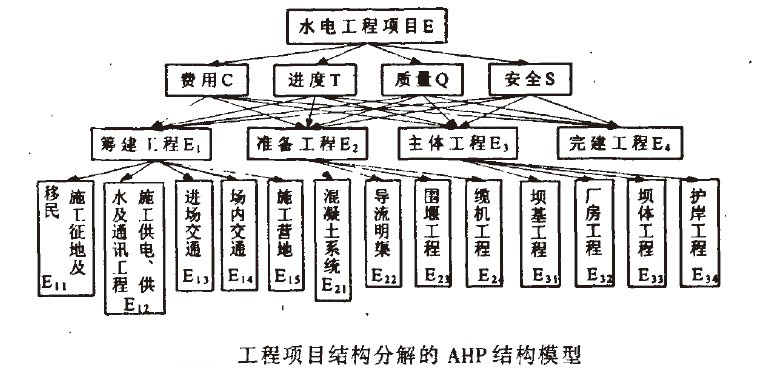
在建立整體工程風險因素網路分析模型結構時，首先要建立工程項目的工作結構模型。由於各個子工程項目都有其相應的工程式控制制目標:費用、進度、質量、安全，並且各個子項目對整體工程項目目標必然具有不同的重要程度影響。因此在建立工程項目的層次結構時，應該將工程目標作為判斷準則對各子工程項目之間重要度進行判斷。在WBS的基礎上建立的各子工程項目重要度模型是AHP結構，如下圖所示例。
- 3.風險因素的網路結構模型
根據風險的來源將風險因素分為自然風險、技術風險、經濟風險、組織管理風險和社會政策風險五個類別。根據這五個類別風險再進行具體的風險因素的劃分。
傳統的風險分析認為風險具有發生概率和損失兩種屬性，但是這種定義顯然不能夠較全面的反映風險的本質，因此張建設將可預測性、可控制性、可轉移性引人到風險屬性中，將風險看作是具有這五種屬性的多維特性對象進行描述。引人多維屬性對風險進行描述可以從不同角度更全面的反映風險因素的特性，但其中可轉移性和可預測性均可在可控制性上反映，所以只須將可控制性進行估計就可以較全面的反映風險的特性，根據研究的需要，分析認為風險估計一般是對負面影響估計，在傳統的二維屬性的基礎上引人“不可控制性”對水電工程項目風險進行評估。
在風險識別過程中，只識別了風險因素，而要建立ANP模型還必須對風險因素之間的互相影響關係進行研究。通過以專家調查或是小組討論方式最終可得到風險因素影響關係，如下表所示。
根據影響關係表，以風險因素的發生概率、損失和不可控制性為準則建立ANP結構模型，見圖3。
要對每個子工程項目的風險因素都建立相應的風險因素ANP結構模型，即可得到工程項目的整體的結構模型，建立的整體風險因素ANP結構模型為多準則、多層次模型。
- 4.基於ANP的水電工程風險分析模型解析
(1）子工程項自重要度的確定。
計算各子工程項目的重要度，由於基於WBS建立的結構模型為AHP形式，所以採用傳統方式很容易對模型進行重要度求解。
(2)子工程的風險因素的權重向量及排序。
對各子工程項目下相互關聯的風險因素權重向量確定是圖3子工程項目風險因素的ANP結構模型。
整個工程項目風險因素排序的關鍵步驟，同時也是採用ANP進行風險分析的核心。根據圖3的ANP結構模型以及表1中的風險因素影響關係，對子工程項目下的風險因素權重計算按以下步驟進行:
1)計算風險屬性權重。對描述風險大小的概率、損失和不可控制性進行重要性比較。此三個屬性是看作評判風險因素的準則，所以採用傳統的AHP法可以確定其權重大小。
2)計算單準則下各風險因素權重。由於此模型是多準則問題，因此相互關聯的風險因素要在三個準則下分別進行比較判斷，現以其中概率準則對風險因素進行研究，這一過程又可分為以下幾步:
a.建立超矩陣。建立以概率為主準則，以其中一個風險因素為次準則，進行其他風險因素的相對重要度比較，即其他風險因素對這一風險因素髮生概率的影響程度大小進行重要度比較。由於並不是其他每個風險因素都對其有影響，所以並不是所有元素都要在此次準則下進行比較，影響這個一風險因素的其他風險因素可從影響關係表中查得。然後以各風險類別組為單元分別計算其特征向量，即相應的局部權重向量。經過以每一個元素為次準則的比較判斷和計算後按式(1)建立超矩陣。
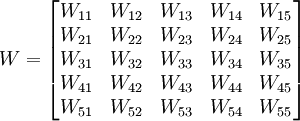(1)
其中(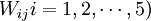
；
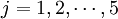))表示風險因素類別Rj中風險因素受Ri類別中因素影響的向量矩陣。Wij的列向量是由Ri中每個因素以Rj中一個因素為次準則，進行比較判斷得到判斷矩陣的特征向量。
b.建立權矩陣。以概率為主準則，風險類別Ri為次準則，對所有類別進行比較判斷構造判斷矩陣，即每個風險類別中的對Ri風險類別發生概率的影響程度大小進行判斷比較。其中的判斷比較包括了Ri自身與其他類別對自身影響的比較判斷。因為每個風險因素所受的影響程度是在各風險類別中進行比較判斷的，由多個矩陣組成的超矩陣中的各列向量不是歸一化的，即列向量和不為1，無法比較分別存在於不同類別中的元素對一個為次準則的因素影響程度的大小;另外，未加權的超矩陣無法採用冪法求解極限相對權重向量，所以要對各風險類別的互相影響重要度進行比較判斷。依次以各個類別為次準則進行比較判斷後，得到五個判斷矩陣，並計算特征向量，最後可得如式(2)的權矩陣。
(2)
c.建立加權超矩陣並求解。將超矩陣按式(3)進行加權可得到加權超矩陣，加權超矩陣中列向量元素大小即為各風險因素對處於此列上的因素影響的大小，若某一風險因素對此因素沒有影響，則對應的值為零。此時可利用冪法或其他方法對加權超矩陣進行相對排序向量的求解，最後相對排序向量就是各風險因素在概率準則下的權重。
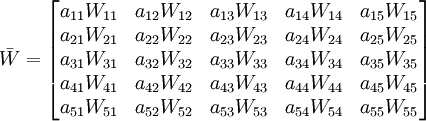(3)
3)計算多準則風險因素權重。依次以損失、不可控制性為準則對各風險因素按照第(2)步進行權重向量求解，然後以第(1)步中所求得的權重對各單準則的風險因素權重進行合成，可得到風險因素在子工程項目中的風險大小排序。
(3)整體工程項目風險因素排序
對每一個子工程項目的風險因素進行權重向量求解，就可以對整體工程項目的風險因素進行權重合成和總排序計算。
將各子工程項目的風險因素權重對應到整體工程項目所有風險因素中，對於不影響此子工程項目的風險因素，將其權重設為零。由上述工程項目重要度的計算，得到了各子工程項目在整體工程項目的權重，因此通過對各層子工程項目下的風險因素權重進行加權求和就可得到各風險因素在上一層工程項目的排序。最終可得到整體工程項目的風險因素總排序。
從總排序結果可以很容易發現工程項目所面臨的最大、最關鍵的風險因素，由於考慮了風險因素的相互影響關係，所以最終結果將更加客觀真實地反映實際情況。
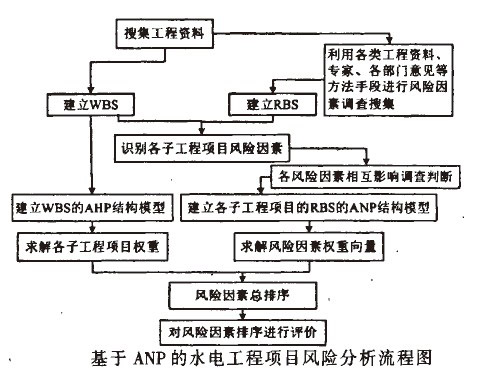
根據上述研究總結得到基於ANP進行水電工程項目風險分析的流程圖，見下圖。
