永久債券
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自永续债券)
永久債券 (Perpetual Bonds)
目錄 |
[編輯]
永久債券也稱無期債券，指的是不規定到期期限，債權人也不能要求清償但可按期取得利息的一種債券。
永久債券的利息一般高於浮動利息，債券的發行人一般多為商業銀行。其發行目的是為了擴充銀行的自有資金實力。
永久性債券與股票的性質相近，可以獲得長期投資資本，但持有者購買的不是股票，因此不能參與企業的經營管理和利潤分配，仍屬於一種間接投資。從債務償還地位來講，當永久債券發行人發生債務危機時，一般債務償還在先，永久債券償還在後。
永久債券的持有者除因發現公司破產或有重大財務事件外，一般不能要求公司償還，而只能定期地獲得利息收入，實際上這種債券以失去了一般公司債的性質，並且具有股票的特征，因而有人認為這是一種最徹底的公司債。在美國有一種期限為數十年甚至百年以上的公司債，也可認為是一種變相的永久公司債。
[編輯]
永久債券的價格的計算[1]
永久債券的價格實際上是在一定貼現率（必要投資收益率）下的未來無數次利息流量現值之和，其定價公式為：
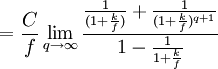
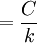
式中，C為票面年利息（等於面值×票面利率），k為貼現率，f為一年內付息次數。
[編輯]
永久債券計算實例[1]
例3 假設有一永久債券，面額為1000元，年利率8%，投資者要求的年投資收益率為10%，問投資者願意接受的價格是多少？
解：已知 C=1000×8%=80元 k=10%，則：
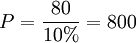（元）
即該債券市場價格只要不超過800元，該投資者就會購買此債券。
[編輯]
[編輯]
