次數直方圖

出自 MBA智库百科(https://wiki.mbalib.com/)

次數直方圖（Frequency histogram）

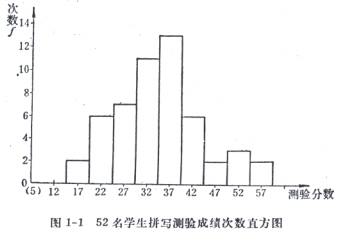
　　次數直方圖是由若幹寬度相等、高度不一的直方條緊密排列在同一基線上構成的圖形。

　　圖1-1便是根據表1中的簡單次數分佈，按一定規則繪製成的次數直方圖。

表1:52名學生拼寫測驗成績分佈統計結果

組別	組中值	劃記	次數()	相對次數	累積次數	累積相對次數	累積百分數
（1）	（2）	（3）	（4）	（5）	（6）	（7）	（8）
55～59	57	2個數據	2	0.04	52	1.00	100
50～54	52	3個數據	3	0.06	50	0.96	96
45～49	47	2個數據	2	0.04	47	0.90	90
40～44	42	6個數據	6	0.11	45	0.86	86
35～39	37	13個數據	13	0.25	39	0.75	75
30～34	32	11個數據	11	0.21	26	0.50	50
25～29	27	7個數據	7	0.14	15	0.29	29
20～24	22	6個數據	6	0.11	8	0.15	15
15～19	17	2個數據	2	0.04	2	0.04	4
			N=52	1.00

　　它的製作步驟可簡述如下：

　　（1）以細線條畫橫軸和縱軸（取正半軸即可），使其垂直相交。為使圖形美觀，通常使橫與縱軸的長度比為5:3。以縱軸為次數的量尺，按比例等間隔地標出刻度,在本例中分別標出0，2，4，…，14為止即可；橫軸代表測驗的分數量尺，也按適當的比例等間隔地標出次數分佈中各組的組中值。一般說來，縱橫軸刻度則需根據最低一組的下限來確定，為了不影響圖形的美觀，通常不從刻度“0”開始。本例是從刻度“5”開始， 併在這一特殊的起點值上加上圓括弧，以示區別。

　　（2）每一直方條的寬度由組距i確定並已體現在橫軸的等距刻度上。直方條的高度由相應組別的次數 多少決定。所有的直方條以各組的組中值為對稱點，沿著橫軸，依順序緊密直立排列。這樣，次數直方圖即告繪成。

　　（3）在直方圖橫軸下邊標上圖的編號和圖的題目， 並檢查一下圖形結構的完整性。

　　與次數分佈表相比較，次數直方圖確實比較直觀形象，使人一目瞭然，尤其能很快地看出各組次數之間的相對大小及結構形態。20世紀80年代中期，某些省的研究人員曾經用次數直方圖來反映專門人才隊伍的年齡結構情況，其次數分佈直方圖所外圍呈“馬鞍”型，表明瞭在特定年齡段上的專門人才隊伍出現低谷區。這種現象以次數直方圖的形式向有關政府部門報告時,就能使人看後產生強烈印象。

　　次數直方圖也有其不足之處，那就是人們不易準確與快速地瞭解到各組的次數大小。為此，在繪製次數直方圖時，有人也把各組的次數分別標在各個直方條的頂端，以便閱讀。

• 次數多邊圖
• 次數分佈表
• 次數分佈圖