林齡

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是林齡^[1]

　　林齡是指林分的年齡。通常以齡級計數。

林齡的表示方法^[1]

　　林齡有兩種表示方法：以林木的平均年齡代表整個林分的年齡，稱為平均年齡；用優勢樹種的平均年齡表示的稱為優勢年齡。根據林分的年齡結構，將林木年齡相同的林分稱為同齡林，而將林木年齡相差超過一個齡級的林分稱為異齡林。此外，根據森林生長髮育的過程又分為幼齡林、壯齡林、中齡林、近熟林、過熟林。

[編輯]

林齡空間與轉移方程^[2]

[編輯]

林齡空間的定義

　　因為森林的林齡結構在森林資源的可持續發展(或永續)中起著重荸望作用，所以研究森林林齡結構的轉移和變化具有重要的意義。由此引出林齡空間的定義。

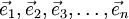
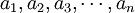
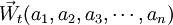
　　[定義]　　設某林區的森林的齡級(狀態)共確n個，其對應的單位面積記為矢量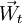： $\vec{e}_1,\vec{e}_2,\vec{e}_3,\ldots ,\vec{e}_n$ 　　顯然它們構成了n維空間的基底。設某時刻t該林區各齡級的森林面積為 $a_1,a_2,a_3,\cdots ,a_n$ 記為 $\vec{W}_t(a_1,a_2,a_3,\cdots ,a_n)$ 稱為該林區t時刻的林齡結構狀態向量，簡稱為林齡向量。記為 $\vec{W}_t$ ，則對所有時刻t，t∈(0,∞)

的林齡向量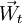 $\vec{W}_t$ 構成集合稱為林齡狀態空間，簡稱林齡空間，記為Φ。

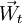　　若某林區的森林齡級(狀態)共有3個，則林齡空間就是普通意義下的三維向量空間，見圖1。一般在n維林齡空間中，某林區的林齡向量 $\vec{W}_t$ ，在自然生長和經營活動的作用下，必然隨著時間的推移做某種運動，由此帶動該林區的森林資源和環境(甚至林區的經濟)不斷地發生變化。這種變化有可能向著森林可持續發展方向變化，也有可能向著森林不可持續發展方向變化。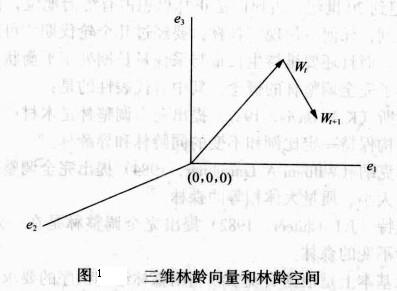

[編輯]

林齡向量的轉移

　　1．轉移概率

　　[定義]　　設某t時刻、第j齡級(記為狀態

E j

)的林分，經過一個分期(1個分期相當於1個齡級)到t+1時刻後轉移到第i齡級(記為狀態

E i

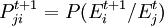
)，其條件概率 $P_{ji}^{t+1}=P(E_i^{t+1}/E_j^t)$ 稱為t+1時刻的一步轉移概率，簡稱轉移概率，記為

P j i (1)

或

P j i

[嚴格寫法是

P j i

(t，t+1)]。

　　同理可定義k步轉移概率，記為 $P j i (k)$ 。由於在一定的假設條件下(齊次)k步轉移概率 $P j i (k)$ 可由一步轉移概率 $P j i (1)$ 導出，因此一般只講一步轉移概率。

　　2．林齡向量的轉移(運動)方式

　　林齡向量非隨機運動方式有下述幾種：

　　(1)自然生長轉移。由於組成林分的林木年齡在不斷地增長，因此林分的平均年齡必然隨之增長。在絕對同齡的(如人工林)林分中，林分齡級經過一個分期必然(以概率1)要長入下一齡級，即林分生長轉移概率 $P j, j + 1 = 1$ 。

　　(2)皆伐轉移。由於皆伐後林分一般在本分期內完成更新(這是森林經營的基本法則)，因此該林分採伐齡級經過一個分期必然(以概率1)要進入1齡級，即林分採伐轉移概率 $P j,1 = 1$ 。

　　(3)擇伐轉移。由於擇伐後一般齡級會下降，下降的幅度依賴於林分條件和擇伐的強度等條件，該林分的擇伐轉移概率 $P j, t = 1$ ，i<j。

　　(4)造林和天然更新轉移概率 $P 0,1 = 1$ 。

　　3．轉移概率矩陣

　　由組成t時刻林齡向量的所有可能的狀態(即齡級)的轉移概率

P j i

組成的矩陣稱為轉移概率矩陣，記為

P t

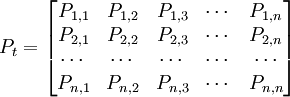
，也叫做一步轉移概率矩陣。一般來說，它與時間t有關。 $P_t=\begin{bmatrix} P_{1,1} & P_{1,2} & P_{1,3} & \cdots & P_{1,n} \\ P_{2,1} & P_{2,2} & P_{2,3} & \cdots & P_{2,n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ P_{n,1} & P_{n,2} & P_{n,3} & \cdots & P_{n,n}\end{bmatrix}$ 　　顯然轉移概率具有性質：0≤

P i j

≤1和

\sum P i j = 1 j

[編輯]

林齡轉移方程

　　設某林區在t分期的林齡向量為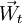 $\vec{W}_t$ ，在一步轉移概率矩陣 $P t$ 作用下，經過一個分期轉移到 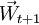$\vec{W}_{t+1}$ ，則

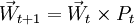
　　 $\vec{W}_{t+1}=\vec{W}_t\times P_t$

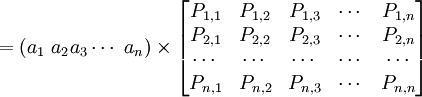
　　 $=(a_1\ a_2 a_3 \cdots \ a_n)\times \begin{bmatrix} P_{1,1} & P_{1,2} & P_{1,3} & \cdots & P_{1,n} \\ P_{2,1} & P_{2,2} & P_{2,3} & \cdots & P_{2,n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ P_{n,1} & P_{n,2} & P_{n,3} & \cdots & P_{n,n}\end{bmatrix}$

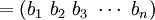　　 $=(b_1\ b_2\ b_3\ \cdots \ b_n)$ 　　(1)

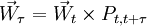　　稱為林齡狀態一步轉移方程。更一般的林齡轉移方程是 $\vec{W}_\tau=\vec{W}_t\times P_{t,t+\tau}$ 　　(2)

　　[例1]　　設某林區的某林齡向量為，只有4個齡級。假設各齡級的皆伐(皆伐後立即更新)概率為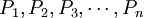 $P_1,P_2,P_3,\cdots ,P_n$ 。求下一分期的林齡向量。

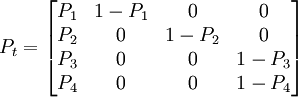
　　解：由各齡級的皆伐概率和保留區的生長，可得該分期的轉移概率矩陣為 $P_t=\begin{bmatrix} P_1 & 1-P_1 & 0 & 0 \\ P_2 & 0 & 1-P_2 & 0 \\ P_3 & 0 & 0 & 1-P_3 \\ P_4 & 0 & 0 & 1-P_4\end{bmatrix}$

　　則有轉移方程

　　 $\vec{W}_{t+1}=(b_1,b_2,b_3,b_4)$

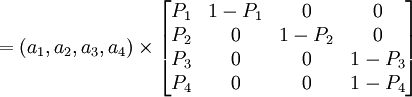
　　 $=(a_1,a_2,a_3,a_4)\times \begin{bmatrix} P_1 & 1-P_1 & 0 & 0 \\ P_2 & 0 & 1-P_2 & 0 \\ P_3 & 0 & 0 & 1-P_3 \\ P_4 & 0 & 0 & 1-P_4\end{bmatrix}$

得林齡向量

　　 $\vec{W}_{t+1}=(b_1\ b_2\ b_3\ b_4)$

$b 1 = a 1 P 1 + a 2 P 2 + a 3 P 3 + a 4 P 4$
$b 2 = a 1 - a 1 P 1$
$b 3 = a 2 - a 2 P 2$
$b 4 = a 3 - a 3 P 3 + a 4 - a 4 P 4$

[編輯]

廣林齡向量

　　以上的林齡向量往往指某一優勢樹種(組)林分的集合，因為它們有統一的齡級距、齡級數和林學特征。而一個林區就由許多這樣韻林齡向量所構成，所以林齡向量和林齡空間就需要擴充。由此引出廣林齡向量的定義。

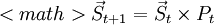　　[定義]　　設某林區由m個樹種(組)的林齡向量所構成，林齡的狀態(即齡級)為0(欲造林的無林地)，1，2，…，n，並設t分期i樹種(組)的林齡向量為 $S^t(i)=[s_0^t(i),s_1^t(i),s_2^t(i),\cdots ,s_n^t(i)]$ 　　i=1,2，3,…,m 　　則該林區在t分期的廣林齡向量為 $\vec{S}_t=[s^t(i),s^t(2),\cdots ,s^t(m)]=[s_0^t(1)\ s_1^t(1)\cdots s_0^t(2)\ s_1^t(2),\cdots ,s_n^t(m)]$ 　　(3) 　　由轉移方程可知該林區在t+1分期的廣林齡向量為 $<math>\vec{S}_{t+1}=\vec{S}_t\times P_t$ 　　(4)

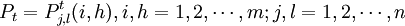　　式中 $P t$ 為： $P_t={P_{j,l}^t(i,h),i,h=1,2,\cdots,m;j,l=1,2,\cdots ,n}$ 。其元素是樹種i向樹種h，齡級j向齡級l的轉移概率，可由實驗數據獲得。

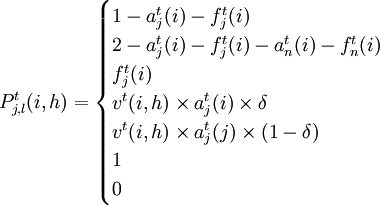$P_{j,l}^t(i,h)=\begin{cases} 1-a_j^t(i)-f_j^t(i) \\ 2-a_j^t(i)-f_j^t(i)-a_n^t(i)-f_n^t(i) \\ f_j^t(i) \\ v^t(i,h)\times a_j^t(i)\times \delta \\ v^t(i,h)\times a_j^t(j)\times (1-\delta) \\ 1 \\ 0 \end{cases}$	當l=j+1<n,i=h,j≥1
	當l=j+1=n,j=h
	當h=i,l是擇伐下降的齡級
	當l=0
	當l=1,j>0
	當l=1,j=0,i=h
	其他

　　式中　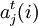　 $a_j^t(i)$ ——第i樹種第，齡級的皆伐比重；

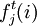　　　　　　 $f_j^t(i)$ ——第i樹種第歹齡級的擇伐比重；

　　　　　　 $v t (i, h)$ ——皆伐第i樹種後，更新第h樹種的更新率；

　　　　　　δ——更新速率，δ=更新期／齡級寬度；

在上式中，擇伐下降的齡級是以擇伐後的蓄積相當於某齡級蓄積來確定的。其中：

第一式是在樹種不變的條件下，小於n齡級的保留林分的生長概率；
第二式是在n齡級時保留林分的生長概率；
第三式是在樹種不變條件下的擇伐概率；
第四式是i樹種皆伐後的用h樹種更新，但齡級仍為0的概率(即造林率)；
第五式是i樹種皆伐後的h樹種更新，且齡級仍為0的概率；
第六式是無林地必需全部更新，且齡級為1。

[編輯]

參考文獻

↑ ^1.0 ^1.1 黃瑞琦主編.林業現代行業語詞典.南海出版公司,2000.12.
↑ 郎奎建,王長文編著.2 森林資源可持續發展特征方程森林經營管理學導論.東北林業大學出版社,2005.8.

取自"https://wiki.mbalib.com/zh-tw/%E6%9E%97%E9%BE%84"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

连晓雾.

頁面分類: 林業

評論(共0條)

提示:評論內容為網友針對條目"林齡"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

林齡

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是林齡^[1]

林齡的表示方法^[1]

林齡空間與轉移方程^[2]

林齡空間的定義

林齡向量的轉移

林齡轉移方程

廣林齡向量

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

∑	P_ij = 1
j

查看

工具▼

林齡

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是林齡[1]

林齡的表示方法[1]

林齡空間與轉移方程[2]

林齡空間的定義

林齡向量的轉移

林齡轉移方程

廣林齡向量

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

什麼是林齡^[1]

林齡的表示方法^[1]

林齡空間與轉移方程^[2]