林龄

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什么是林龄^[1]

　　林龄是指林分的年龄。通常以龄级计数。

林龄的表示方法^[1]

　　林龄有两种表示方法：以林木的平均年龄代表整个林分的年龄，称为平均年龄；用优势树种的平均年龄表示的称为优势年龄。根据林分的年龄结构，将林木年龄相同的林分称为同龄林，而将林木年龄相差超过一个龄级的林分称为异龄林。此外，根据森林生长发育的过程又分为幼龄林、壮龄林、中龄林、近熟林、过熟林。

[编辑]

林龄空间与转移方程^[2]

[编辑]

林龄空间的定义

　　因为森林的林龄结构在森林资源的可持续发展(或永续)中起着重荸望作用，所以研究森林林龄结构的转移和变化具有重要的意义。由此引出林龄空间的定义。

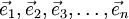
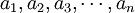
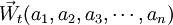
　　[定义]　　设某林区的森林的龄级(状态)共确n个，其对应的单位面积记为矢量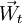： $\vec{e}_1,\vec{e}_2,\vec{e}_3,\ldots ,\vec{e}_n$ 　　显然它们构成了n维空间的基底。设某时刻t该林区各龄级的森林面积为 $a_1,a_2,a_3,\cdots ,a_n$ 记为 $\vec{W}_t(a_1,a_2,a_3,\cdots ,a_n)$ 称为该林区t时刻的林龄结构状态向量，简称为林龄向量。记为 $\vec{W}_t$ ，则对所有时刻t，t∈(0,∞)

的林龄向量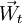 $\vec{W}_t$ 构成集合称为林龄状态空间，简称林龄空间，记为Φ。

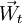　　若某林区的森林龄级(状态)共有3个，则林龄空间就是普通意义下的三维向量空间，见图1。一般在n维林龄空间中，某林区的林龄向量 $\vec{W}_t$ ，在自然生长和经营活动的作用下，必然随着时间的推移做某种运动，由此带动该林区的森林资源和环境(甚至林区的经济)不断地发生变化。这种变化有可能向着森林可持续发展方向变化，也有可能向着森林不可持续发展方向变化。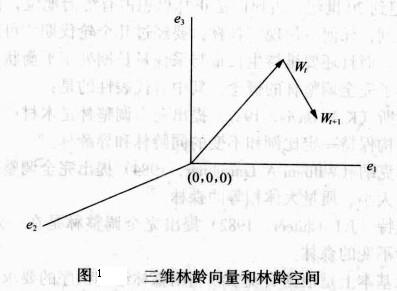

[编辑]

林龄向量的转移

　　1．转移概率

　　[定义]　　设某t时刻、第j龄级(记为状态

E j

)的林分，经过一个分期(1个分期相当于1个龄级)到t+1时刻后转移到第i龄级(记为状态

E i

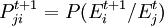
)，其条件概率 $P_{ji}^{t+1}=P(E_i^{t+1}/E_j^t)$ 称为t+1时刻的一步转移概率，简称转移概率，记为

P j i (1)

或

P j i

[严格写法是

P j i

(t，t+1)]。

　　同理可定义k步转移概率，记为 $P j i (k)$ 。由于在一定的假设条件下(齐次)k步转移概率 $P j i (k)$ 可由一步转移概率 $P j i (1)$ 导出，因此一般只讲一步转移概率。

　　2．林龄向量的转移(运动)方式

　　林龄向量非随机运动方式有下述几种：

　　(1)自然生长转移。由于组成林分的林木年龄在不断地增长，因此林分的平均年龄必然随之增长。在绝对同龄的(如人工林)林分中，林分龄级经过一个分期必然(以概率1)要长入下一龄级，即林分生长转移概率 $P j, j + 1 = 1$ 。

　　(2)皆伐转移。由于皆伐后林分一般在本分期内完成更新(这是森林经营的基本法则)，因此该林分采伐龄级经过一个分期必然(以概率1)要进入1龄级，即林分采伐转移概率 $P j,1 = 1$ 。

　　(3)择伐转移。由于择伐后一般龄级会下降，下降的幅度依赖于林分条件和择伐的强度等条件，该林分的择伐转移概率 $P j, t = 1$ ，i<j。

　　(4)造林和天然更新转移概率 $P 0,1 = 1$ 。

　　3．转移概率矩阵

　　由组成t时刻林龄向量的所有可能的状态(即龄级)的转移概率

P j i

组成的矩阵称为转移概率矩阵，记为

P t

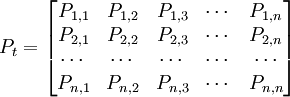
，也叫做一步转移概率矩阵。一般来说，它与时间t有关。 $P_t=\begin{bmatrix} P_{1,1} & P_{1,2} & P_{1,3} & \cdots & P_{1,n} \\ P_{2,1} & P_{2,2} & P_{2,3} & \cdots & P_{2,n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ P_{n,1} & P_{n,2} & P_{n,3} & \cdots & P_{n,n}\end{bmatrix}$ 　　显然转移概率具有性质：0≤

P i j

≤1和

\sum P i j = 1 j

[编辑]

林龄转移方程

　　设某林区在t分期的林龄向量为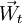 $\vec{W}_t$ ，在一步转移概率矩阵 $P t$ 作用下，经过一个分期转移到 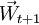$\vec{W}_{t+1}$ ，则

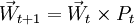
　　 $\vec{W}_{t+1}=\vec{W}_t\times P_t$

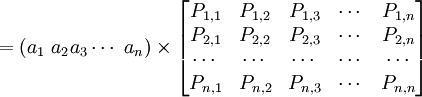
　　 $=(a_1\ a_2 a_3 \cdots \ a_n)\times \begin{bmatrix} P_{1,1} & P_{1,2} & P_{1,3} & \cdots & P_{1,n} \\ P_{2,1} & P_{2,2} & P_{2,3} & \cdots & P_{2,n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ P_{n,1} & P_{n,2} & P_{n,3} & \cdots & P_{n,n}\end{bmatrix}$

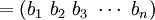　　 $=(b_1\ b_2\ b_3\ \cdots \ b_n)$ 　　(1)

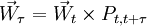　　称为林龄状态一步转移方程。更一般的林龄转移方程是 $\vec{W}_\tau=\vec{W}_t\times P_{t,t+\tau}$ 　　(2)

　　[例1]　　设某林区的某林龄向量为，只有4个龄级。假设各龄级的皆伐(皆伐后立即更新)概率为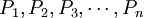 $P_1,P_2,P_3,\cdots ,P_n$ 。求下一分期的林龄向量。

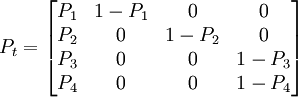
　　解：由各龄级的皆伐概率和保留区的生长，可得该分期的转移概率矩阵为 $P_t=\begin{bmatrix} P_1 & 1-P_1 & 0 & 0 \\ P_2 & 0 & 1-P_2 & 0 \\ P_3 & 0 & 0 & 1-P_3 \\ P_4 & 0 & 0 & 1-P_4\end{bmatrix}$

　　则有转移方程

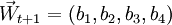
　　 $\vec{W}_{t+1}=(b_1,b_2,b_3,b_4)$

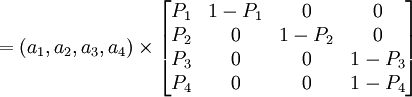
　　 $=(a_1,a_2,a_3,a_4)\times \begin{bmatrix} P_1 & 1-P_1 & 0 & 0 \\ P_2 & 0 & 1-P_2 & 0 \\ P_3 & 0 & 0 & 1-P_3 \\ P_4 & 0 & 0 & 1-P_4\end{bmatrix}$

得林龄向量

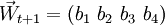
　　 $\vec{W}_{t+1}=(b_1\ b_2\ b_3\ b_4)$

$b 1 = a 1 P 1 + a 2 P 2 + a 3 P 3 + a 4 P 4$
$b 2 = a 1 - a 1 P 1$
$b 3 = a 2 - a 2 P 2$
$b 4 = a 3 - a 3 P 3 + a 4 - a 4 P 4$

[编辑]

广林龄向量

　　以上的林龄向量往往指某一优势树种(组)林分的集合，因为它们有统一的龄级距、龄级数和林学特征。而一个林区就由许多这样韵林龄向量所构成，所以林龄向量和林龄空间就需要扩充。由此引出广林龄向量的定义。

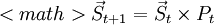　　[定义]　　设某林区由m个树种(组)的林龄向量所构成，林龄的状态(即龄级)为0(欲造林的无林地)，1，2，…，n，并设t分期i树种(组)的林龄向量为 $S^t(i)=[s_0^t(i),s_1^t(i),s_2^t(i),\cdots ,s_n^t(i)]$ 　　i=1,2，3,…,m 　　则该林区在t分期的广林龄向量为 $\vec{S}_t=[s^t(i),s^t(2),\cdots ,s^t(m)]=[s_0^t(1)\ s_1^t(1)\cdots s_0^t(2)\ s_1^t(2),\cdots ,s_n^t(m)]$ 　　(3) 　　由转移方程可知该林区在t+1分期的广林龄向量为 $<math>\vec{S}_{t+1}=\vec{S}_t\times P_t$ 　　(4)

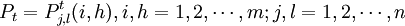　　式中 $P t$ 为： $P_t={P_{j,l}^t(i,h),i,h=1,2,\cdots,m;j,l=1,2,\cdots ,n}$ 。其元素是树种i向树种h，龄级j向龄级l的转移概率，可由实验数据获得。

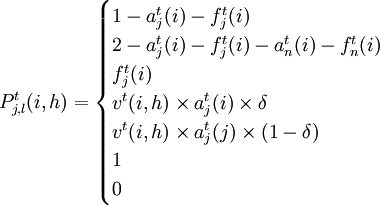$P_{j,l}^t(i,h)=\begin{cases} 1-a_j^t(i)-f_j^t(i) \\ 2-a_j^t(i)-f_j^t(i)-a_n^t(i)-f_n^t(i) \\ f_j^t(i) \\ v^t(i,h)\times a_j^t(i)\times \delta \\ v^t(i,h)\times a_j^t(j)\times (1-\delta) \\ 1 \\ 0 \end{cases}$	当l=j+1<n,i=h,j≥1
	当l=j+1=n,j=h
	当h=i,l是择伐下降的龄级
	当l=0
	当l=1,j>0
	当l=1,j=0,i=h
	其他

　　式中　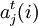　 $a_j^t(i)$ ——第i树种第，龄级的皆伐比重；

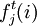　　　　　　 $f_j^t(i)$ ——第i树种第歹龄级的择伐比重；

　　　　　　 $v t (i, h)$ ——皆伐第i树种后，更新第h树种的更新率；

　　　　　　δ——更新速率，δ=更新期／龄级宽度；

在上式中，择伐下降的龄级是以择伐后的蓄积相当于某龄级蓄积来确定的。其中：

第一式是在树种不变的条件下，小于n龄级的保留林分的生长概率；
第二式是在n龄级时保留林分的生长概率；
第三式是在树种不变条件下的择伐概率；
第四式是i树种皆伐后的用h树种更新，但龄级仍为0的概率(即造林率)；
第五式是i树种皆伐后的h树种更新，且龄级仍为0的概率；
第六式是无林地必需全部更新，且龄级为1。

[编辑]

参考文献

↑ ^1.0 ^1.1 黄瑞琦主编.林业现代行业语词典.南海出版公司,2000.12.
↑ 郎奎建,王长文编著.2 森林资源可持续发展特征方程森林经营管理学导论.东北林业大学出版社,2005.8.

来自"https://wiki.mbalib.com/wiki/%E6%9E%97%E9%BE%84"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

连晓雾.

页面分类: 林业

评论(共0条)

提示:评论内容为网友针对条目"林龄"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

林龄

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是林龄^[1]

林龄的表示方法^[1]

林龄空间与转移方程^[2]

林龄空间的定义

林龄向量的转移

林龄转移方程

广林龄向量

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

∑	P_ij = 1
j

查看

工具箱▼

林龄

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是林龄[1]

林龄的表示方法[1]

林龄空间与转移方程[2]

林龄空间的定义

林龄向量的转移

林龄转移方程

广林龄向量

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

什么是林龄^[1]

林龄的表示方法^[1]

林龄空间与转移方程^[2]