多因數模型
出自 MBA智库百科(https://wiki.mbalib.com/)
- 多因數模型(Multifactor Model)
目錄 |
什麼是多因數模型[1]
多因數模型是關於資產定價的模型。與資本資產定價模型和單指數模型不同,多因數模型認為證券價格並不僅僅取決於證券的風險,還取決於其他一些因素,如,投資者未來預期收入、未來消費品的相對價格及未來的投資機會等。
多因數模型的理論背景是Ross基於套利原理創立的套利定價理論(APT)和Merton基於均衡原理創立的跨時期資本資產定價模型(ICAPM)。
多因數模型的基本形式[2]

式中:δkt——第是個風險因素在時期,的意外變化;bik資產i對第是個風險因素的敏感繫數。
多因數模型的種類[3]
- 第一,Brennan—Schwartz模型
Brennan—Schwartz模型運用短期和長期利率作為因數解釋利率期限結構。短期利率對長期均衡有均值回覆的效應,並遵循對數正態過程,長期利率遵循另外的對數正態過程,即:
dlnr = a(lnl − lnr)dt + b1W1
dl = la(r,l,b2)dt + b2ldW2
其中E[dW1dW2] = pdt.從模型中無法直接得到債券價格的封閉解,必須求解其數值解。
- 第二,Richard模型
Richard模型運用實際利率ρ和通貨膨脹率π作為兩種因數,兩者相互獨立,並遵循以下平方根過程:
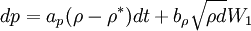
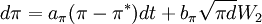
r = ρ + π(1 − var[dP / P])
其中,P表示預期變化為通貨膨脹率的價格。因而名義債券價格的解為:
![P(t,T)=\hat{E}_t[exp(-\int_t^T r(u)du)]=\hat{E}_t[exp(-\int_t^T \rho(u)du)] \hat{E}_t[exp(-\int_t^T \pi(u)du)] exp(1-V_P)](/w/images/math/c/7/4/c7403a7bb5d4adeb20074b4f1ced4901.png)
- 第三,Cox-Ingersoll-Ross/Langetieg模型
1985年,Cox,Ingersoll和Ross又發展了兩因數模型,認為利率的變化除了短期利率的隨機過程外,還存在長期利率的隨機過程。遵循CIR模型的思路,瞬時利率r可以分解成兩個獨立的因數Y1和Y2(即r = y1 + y2),則關於債券價格的解為:
![P(t,T)=\hat{E}_t{exp[-\int_t^T r(u)du]}=\hat{E}_t{exp[-\int_t^T y_1(u)du]} \hat{E}_t{exp[-\int_t^T y_2(u)du]}=P_1(t,T)P_2(t,T)](/w/images/math/b/9/c/b9ce9f13d3bb2e7e4a1170401a792d7d.png)
如果每一因數都遵循Vasicek假設,那麼其中每一個P值都會有單因數解;如果每一因數都遵循CIR假設,那麼債券價格將是兩個CIR公式的乘積。
- 第四,Longstaff-Schwartz模型
Longstaff-Schwartz模型與CIR模型的區別在於它將無法觀測到的因數映射為在確定利率期限結構中重要的可觀測的因數.其中兩種狀態變數可以寫成:
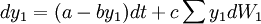
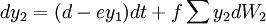
其中,dW1dW2 = 0,根據CIR,均衡的利率水平及其波動率為:
r = αy1 + βy2
r = α2y1 + β2y2
運用伊騰法則(Ito's lemma)解聯立方程,得到dr和dV的表達式,從而得到債券價格的封閉解。







