利率上限
出自 MBA智库百科(https://wiki.mbalib.com/)
利率上限(interest rate cap)
目錄 |
什麼是利率上限[1]
利率上限是指買賣雙方就未來某一時期商定一個固定利率作為利率上限,如果協議規定的市場利率(通常為LIBOR)超過上限利率,則由賣方將市場利率與上限利率的差額支付給買方,但買方在協議簽訂時,必須支付賣方一定費用。
具有浮動利率負債的債務人,或具有固定利率存款的債權人,為防止利率風險,固定債務(權)的支出(或收入),常使用這一工具,以規避風險,核算成本。
利率上限的定價[2]
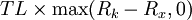
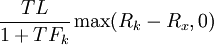
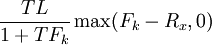
這樣,我們就可將一個利率上限看作由若幹期限期權組成,每個期權的標的物為一關於Fk的遠期利率合約,期限從時間。到kT,本金金額為TL / (1 + TFk),執行價格為Rx。
如果我們假設在期權期限內,Fk的標準方差σF恆定不變,那麼根據期貨期權的B-S定價模型,每個期權的價格為:![\frac{TL}{1+TF_k}e^{-rkt}[F_kN(d_1)-R_xN(d_2)]](/w/images/math/9/7/3/973bce3ea7a6346b46628c789d68a92a.png) (1)
(1)其中:
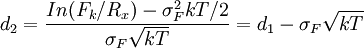
在計算出所有期權價格後,將其相加,我們便得到一個利率上限的價格。
B-S定價模型的一個假設便是σF恆定,這充其量是對實際情況一種近似。如果一個遠期合約距到期日時間較長,F對當前利率變化並不敏感,其標準差σF也較低。但是隨著遠期合約逐漸趨近到期日,F就變得對當前利率變化越來越敏感,σF也隨之不斷增加。
在實踐中,人們採用以下步驟來彌補B-S模型的不足:首先,將B-S模型應用於歐洲美元期貨期權,反解出期貨期權報價所暗含的σF。歐洲美元期貨期權的期限應與所要計算的期權的期限一樣,其次,將此σF代入B-S模型再去求解利率上限中期權的價格。這種以實際市場交易價格中反求σF的方法,可以降低模型所帶來的誤差。
當利率上限所含的某種期權的期限超過所有歐洲美元期貨期權寸,我們就只能用插值法來估計其σF了。有些時候,實務操作人員設定一個適用於所有期權的σF,然後根據各期權的期限長度對其進行調整。調整後的σF才被用於實際計算。
利率上限的運用[3]
在一筆利率上限交易中,交易雙方通常需要明確以下主要內容。
交易貨幣和金額:通常是借款人的借款本金。
有效期限:借款人需要防範利率風險的期限。
執行價格:借款人可以承擔的最高利率水平。
付息期限:借款人付息的期限,即每個設定日期間的時間間隔,通常採用倫敦同業放款利率的期限,如3個月付息一次,6個月付息一次等等。
參考利率:作為市場利率水平,通常採用各期的倫敦同業放款利率。
利率上限的期權費通常採取一次性方式支付,其報價與利率期權的期權費報價方式有所不同。如借款人買入一項利率上限,金額1000萬美元,有效期限為3年,執行價格6%,參考利率為3個月倫敦同業放款利率,期權費報價為1.5%。則實際需支付的期權費金額為:
10000000×1.5%=150000(美元)
利率上限的有效期限內可確定若幹個利息支付日,在每次資金交割時,賣方向買方支付的交割金額計算如下: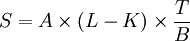
其中,S:每期交割金額;
A:利率上限交易金額;
L:參考利率水平;
K:執行價格;
T:每個付息期限的天數;
B:1年的天數,取360或365,根據不同的貨幣和不同的市場慣例而定。
當L大於K時,賣方向買方支付S金額,當L小於或等於K時,交易雙方不發生資金收付。利率上限每一期的交割金額通常在期末才發生。但在某些情況下,交易雙方可約定在期初支付,此時交割金額必須按參考利率計算出期初的貼現金額,其原理同遠期利率協議相同。








interest rate swaps不是只交換利息嗎?為什麼這裡要用到本金?