凈現值率排序法
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
[編輯]
所謂凈現值率排序法，是指將凈現值率大於或等於零的各個方案按凈現值率的大小依次排序，並依次序選取方案，直至所選取的組合方案的投資總額最大限度地接近或等於投資限額為止。
[編輯]
例：有A、B、C三個獨立的方案，其凈現金流量情況見表1所示，已知總投資限額為800萬元，iC=10%，試利用凈現值率排序法選出最佳投資方案。
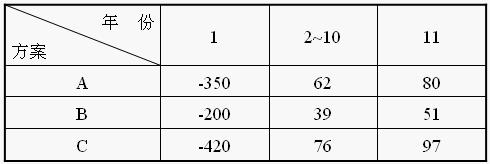
表1 A、B、C三方案的凈現金流量表
解：首先，計算A、B、C三個方案的凈現值率：
各方案投資現值(KP)分別為：
KPA＝-350×(P/F，10%，1)＝318.19(萬元)
KPB＝-200×(P/F，10%，1)＝181.82(萬元)
KPC＝-420×(P/F，10%，1)＝381.82(萬元)
- NPVRA=NPVA/KPA=10.83%
- NPVRB=NPVB/KPB=22.13%
- NPVRC=NPVC/KPC=13.12%
然後，將各方案按凈現值率從大到小依次排序，結果如表2所示。
| 方案 | 凈現值率（%） | 投資額 | 累計投資額 |
|---|---|---|---|
| B | 22.13 | 200 | 200 |
| C | 13.12 | 420 | 620 |
| A | 10.83 | 350 | 970 |
根據表2可知，方案的選擇順序是B→C→A。由於資金限額為800萬元，故最佳投資決策方案為B、C組合。
[編輯]
凈現值率排序法的優點是計算簡便，選擇方法簡明扼要；缺點是由於投資方案的不可分性，經常會出現資金沒有被充分利用的情況，因而不一定能保證獲得最佳組合方案。
[編輯]
