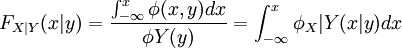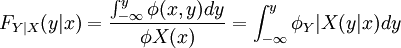二元隨機變數
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
有很多隨機試驗往往會設計2個隨機變數,值得註意的是,這些隨機變數並非孤立,而是相互之間有一定的聯繫。因而需要把它們作為一個整體來研究。如果每次試驗結果都對應著一組確實的實數,它們是隨試驗結果不同變化的二個隨機變數,並且對任何一組實數x1,x2,...,xn,事件有確定的概率,則稱二個隨機變數的整體為一個二元隨機變數。
(1)聯合分佈律
P(X = xi,Y = Yj) = pi,j和下麵的聯合概率分佈表稱作二元離散型隨機變數(X,Y)的分佈律或X與Y的聯合分佈律。pi,j稱為(X,Y)的概率函數或概率分佈,或稱為X和Y的聯合概率函數或概率分佈。
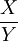
y1 y2 … yj … P(X = xi) X1 p11 p12 … p1j … 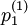
X2 p21 p22 … p2j … 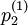
... Xi pi1 pi2 … pij … 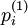
... P(Y=y) 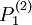
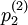
… 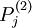
…
(2)邊緣分佈
設(X,Y)具有P(X = xi,Y = Yj) = pij,則
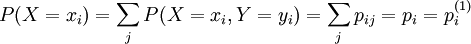 (聯合分佈表中第i行各概率相加)
(聯合分佈表中第i行各概率相加)
稱為(X,Y)對X的邊緣概率分佈。
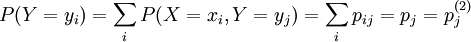 (聯合分佈表中第j列各概率相加)
(聯合分佈表中第j列各概率相加)
稱為(X,Y)對Y的邊緣概率分佈。
(3)條件分佈
對於二元離散型隨機變數(X,Y),如果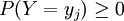 ,則
,則
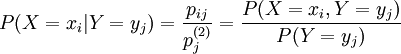
稱為在Y = yj條件下關於X的條件分佈。
同理,如果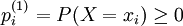 ,則
,則
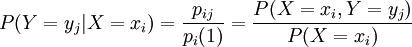
稱為在X = xi條件下關於Y的條件分佈。
(4)二元離散型隨機變數的分佈函數
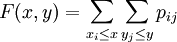
(1)聯合概率密度
如果存在非負函數φ(x,y),使得(X,Y)的分佈函數F(x, y)對於任意實數x, y都有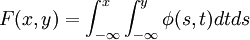 ,
,
則稱(X,Y)是二元連續型隨機變數,φ(x,y)稱為X與Y的聯合概率密度或(X,Y)的概率密度。
分佈函數其實就是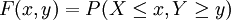 。
。
若φ(x,y)在某區域連續,則對該區域中的每一點(x,y)都有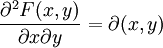
(2)邊緣概率密度
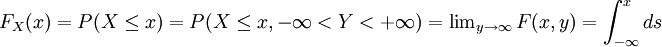

則稱為(X,Y)關於X的邊緣分佈函數。
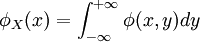 稱為(X,Y)關於X的邊緣概率密度。
稱為(X,Y)關於X的邊緣概率密度。
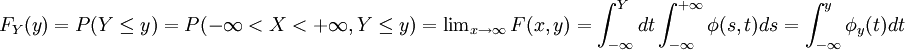
則稱為(X,Y)關於Y的邊緣分佈函數。
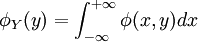 稱為(X,Y)關於Y的邊緣概率密度。
稱為(X,Y)關於Y的邊緣概率密度。
(3)條件概率密度
若φY(y) > 0,稱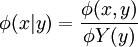 為在Y=y條件下關於X的條件概率密度。
為在Y=y條件下關於X的條件概率密度。
若φX(x) > 0,稱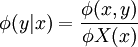 為在X=x條件下關於Y的條件概率密度。
為在X=x條件下關於Y的條件概率密度。
條件分佈函數為: