喬頓的貨幣供給理論
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
喬頓的貨幣供給理論簡介[1]
20世紀60年代末,美國經濟學家喬頓 (Jerry L Jordan,1941年11月12日—)發展了弗里德曼—施瓦茲和卡甘的貨幣供給理論,導出了較為複雜的貨幣乘數模型。在喬頓模型中,貨幣只包括公眾手持通貨和私人活期存款,即狹義的貨幣定義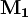 。同時,喬頓模型還區分了聯儲成員銀行和非聯儲成員銀行,區分了受制於不同法定准備金率的不同類型的存款。
。同時,喬頓模型還區分了聯儲成員銀行和非聯儲成員銀行,區分了受制於不同法定准備金率的不同類型的存款。
根據喬頓的分析,在美國,決定貨幣存量的要素為貨幣基數、聯儲成員銀行的準備金與存款之比、通貨與活期存款之比、定期存款與活期存款之比、美國政府存款與私人活期存款之比。這些要素與貨幣供給之間關係具體可以表述為:
假設:
- B——貨幣基數,基礎貨幣
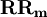 ——聯儲成員銀行的法定准備金
——聯儲成員銀行的法定准備金
 ——聯儲成員銀行的超額準備金
——聯儲成員銀行的超額準備金
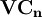 ——非聯儲成員銀行的庫存現金
——非聯儲成員銀行的庫存現金
- R——商業銀行的準備金總額
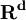 ——聯儲成員銀行活期存款準備金
——聯儲成員銀行活期存款準備金
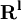 ——聯儲成員銀行定期存款準備金
——聯儲成員銀行定期存款準備金
- C——公眾手持通貨
- D——商業銀行的私人活期存款
- T——商業銀行的私人定期存款
- G——政府存款
- r——各種存款的加權平均準備率
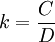 ——現金比率,通貨比率
——現金比率,通貨比率
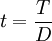 ——定期存款比率
——定期存款比率
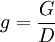 ——政府存款比率
——政府存款比率
則有:狹義貨幣M=C+D
B=C+R
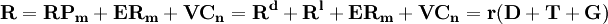 (1)
(1)
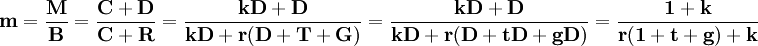 (2)
(2)
式(2)就是喬頓的貨幣乘數模型。根據這一模型,貨幣乘數m是行為參數r、t和g的遞減函數。這意味著,商業銀行各種存款的平均準備率、定期存款比率和政府存款比率的變化將對貨幣乘數產生反向的影響。對於通貨比率對貨幣乘數的影響,從式(2)難以直觀做出判斷。但若就貨幣乘數對通貨比率求偏導則可以發現,在一般情況下,貨幣乘數m是通貨比率k的遞減函數,即通貨比率的變動會引起貨幣乘數的反方向的變動。當然,各行為參數對貨幣乘數的決定並不是完全獨立的,而是相互影響的。例如,若t比率因活期存款增加或定期存款減少而下降,平均準備金比率,一就會上升,因為活期存款的準備率高於定期存款的準備率。t比率的下降使貨幣乘數擴大,而r比率的上升則使貨幣乘數縮小。貨幣乘數究竟會擴大還是縮小,將取決於這兩種比率的變化對貨幣乘數影響的相對大小。[1]
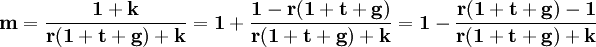
由以上分析可知,喬頓模型中的貨幣乘數是由多種複雜因素共同決定的,而這些因素又分別受到貨幣當局(主要是中央銀行)、商業銀行及社會公眾等不同的經濟主體的行為的影響。由此可見,貨幣當局或中央銀行實際上只能對決定貨幣乘數的部分因素而不是全部因素具有控制能力。也就是說,除了中央銀行以外,商業銀行和社會公眾等其他經濟主體的行為也將對貨幣乘數,從而對貨幣供給產生一定的影響,甚至產生比較重要的影響。這就說明,貨幣供給並不是一個完全決定於貨幣當局的主觀意志,而不受經濟運行的內在規律影響的外生變數。[2]







