一次支付
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
一次支付又稱整付,是指所分析的系統的現金流量,無論是流入還是流出均在某一個時點上一次發生。
一次支付包括兩個計算公式:
(1)一次支付終值複利公式
如果有一筆資金,按年利率i進行投資,n年後本利和應該是多少?也就是已知P,i,n,求終值F。解決此類問題的公式稱為一次支付終值公式,其計算公式是:
F = P(1 + i)n (1)
上式表示在利率為i,計息期數為n條件下,終值F和現值P之間的等值關係。
一次支付終值公式的現金流量圖:
(1+i)n又稱為終值繫數,記為(F/P,i,n)。
於是F=P(F/P,i,n) (2)
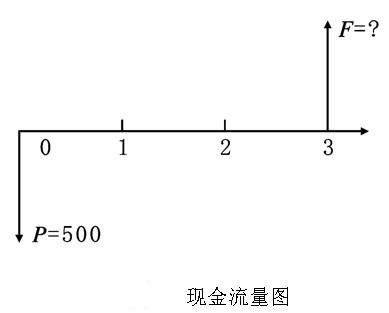
【例1】現在把500元存入銀行,銀行年利率為4%,計算3年後該筆資金的實際價值。
【解】這是一個已知現值求終值的問題,其現金流量圖如下:
由公式(1)可得:
F=P(1+i)3=500×(1+4%)3=562.43(元)
即500元資金在年利率為4%時,經過3年後變為562.43元,增值62.43元。
這個問題也可以利用公式(2)查表計算求解。
由複利繫數表(見附錄)可查得:(F/P,4%,3)=1.1249
所以,F=P(F/P,i,n)=P(F/P,4%,3)=500×1.1249=562.45(元)
(2)一次支付現值複利公式
如果我們希望在n年後得到一筆資金F,在年利率為i的情況下,現在應該投資多少?也即是已知F,i,n,求現值P。解決此類問題用到的公式稱為一次支付現值公式,其計算公式為:
P = F(1 + i)n (3)
其現金流量圖:
在公式(3)中,(1+i)-n又稱為現值繫數,記為(P/F,i,n),它與終值繫數(F/P,i,n)互為倒數,可通過查表求得。因此,公式(3)又可寫為:
P=F(P/F,i,n) (4)
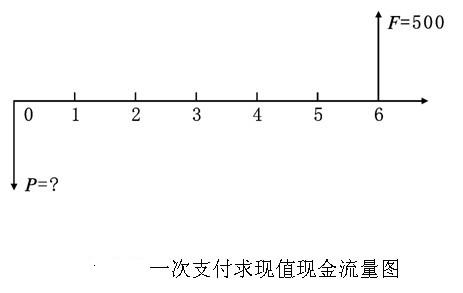
【例2】某企業6年後需要一筆500萬元的資金,以作為某項固定資產的更新款項,若已知年利率為8%,問現在應存入銀行多少錢?
【解】這是一個根據終值求現值的問題,其現金流量圖如下圖:
根據公式(3)可得:
P=F(1+i)^n=500×(1+8%)-6=315.10(萬元)
即現在應存入銀行315.10萬元。
也可以通過查表,根據公式(4)得出。從附表可查得:(P/F,8%,6)=0.6302
所以,P=F(P/F,i,n)=F(P/F,8%,6)=5315.10(萬元)