金融物理学

出自 MBA智库百科(https://wiki.mbalib.com/)

金融物理学(Financial Physics)

　　金融物理学是用统计物理、理论物理、复杂系统理论、非线性科学、应用数学等的概念、理论和方法研究金融市场，通过自组织而涌现的宏观规律及其复杂性的一门新兴交叉学科。简而言之，金融物理学家将金融市场看作一个复杂系统，其中的各种数据（如个股价格、指数、房价等）看作是物理实验数据，力图寻找和阐释其中的物理规律。

　　金融物理学的主要研究内容包括四个方面，其中的大部分内容在本书的后续章节会进行深入介绍。需要指出的是，中国科学技术大学的李平等人也给出了一个十分类似的分类(李平、汪秉宏、全宏俊：《金融物理的若干问题与研究进展(I)：价格的统计分析与价格涨落的随机过程模拟》，《物理》，2004，33(1)：28～33)。

　　第一，金融市场变量(包括收益率、波动率等)的统计规律，特别是金融市场中涌现的具有普适性的标度律，其中最基本的性质是关于收益率的尖峰胖尾分布。

　　第二，证券的相关性、极端事件、金融风险管理和投资组合等。分形市场假说研究相关变量(特别是收益率)的长期记忆性，或自相关性，认为价格演化中存在自相似结构。多重分形理论和方法也被广泛应用于金融市场时间序列的分析。

　　第三，宏观市场的建模和预测，包括用随机过程对收益率建模和对数周期性幂律模型等。对数周期性幂律模型是基于交易者之间的相互模仿，这些局部相互作用可形成正反馈，从而导致泡沫和反泡沫的产生，因此可用于金融泡沫和反泡沫的建模和预测。对数周期性幂律模型可分为两大类，即维尔斯特拉斯族模型和朗道族模型。

　　第四，金融市场的微观模型，主要包括基本面投资者和噪声交易者博弈、逾渗模型(Percolation Models)、伊辛模型(Ising Models)、少数者博弈模型(Minority Games)等，以及由此而衍生出来的各种模型。通过对微观模型的模拟研究，可以深入了解金融市场的微观结构和价格形成机制。

　　一、概率分布

　　概率分布是金融市场变量的最本质也是最重要的统计性质，特别是收益率的概率分布，在各种资产定价模型中处于核心地位。鉴于概率密度函数、特征函数和矩函数之间的等价变换关系，金融变量高阶矩可能呈现的标度不变性和多重分形特性，反映了其概率分布的标度不变性。

　　1900年，Bachelier首次应用布朗运动来描述股票价格演化。20世纪前半叶，一些学者对布朗运动模型进行了理论和实证研究，但是由于计算能力的限制，所得结论的统计意义并不显著。1959年，Osborne发表论文指出，1955～1956年在纽约证交所交易的上千只股票的月度收益率和年度收益率以及道琼斯指数在1916-56年期间的月度收益率都服从高斯分布，他还用更多的数据来验证布朗运动模型。Fama将之称为Bachelier-Osbome模型。

　　1963年，Mandelbrot创造性地应用帕雷托定律描述投机市场价格收益率的尾分布，随后指出平稳帕雷托分布可以比高斯分布更好地刻划棉花价格波动的概率分布，彻底颠覆了布朗运动模型，并引起了经济学界的极大关注。1995年，Mantegna和Stanley将截尾列维分布用于S&P 500指数高频数据的建模，发现收益率在6个方差范围内可以用列维分布很好拟合。可以说，Mantegna和Stanley发表于1995年的这一开创性工作，正式拉开了金融物理学研究的大幕，吸引了大批物理学家加入到相关研究中来。

　　1998年，Gopikrishnan等人分析了美国股市的个股和指数的收益率(时间间隔从5分钟至120分钟)，发现其尾分布具有幂律形式，正尾指数略大于负尾指数，其值都接近-3，被称为负三次方定律。近几年来，很多论文报道了各种不同金融市场中的不同变量服从负三次方定律或幂律尾分布，然而令人担忧的是，其中有些结论是基于很窄的无标度区，是不可靠的。事实上，对有些情形采用拉伸指数分布更为合适。

　　收益率分布的“尖峰胖尾”形态可从不同时间间隔时的概率密度演化的角度来体现。描述概率密度在不同尺度下的演化规律的方法很多，比如湍流研究中的变分理论，它假设收益率的概率密度是给定方差收益率的概率密度的线性叠加，即

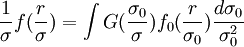
　　式中f是方差为σ标准化收益率r / σ的概率密度，f₀是方差为σ₀标准化收益率r / σ₀的概率密度，G为σ的概率密度函数。这一概率密度演化模型和有限方差从属模型和混合正态模型在有相通处，在描述金融市场收益率演化和间歇性方面十分成功。

　　二、相关性与分形市场假说

　　有效市场假说是金融市场研究的一个重要概念，其核心思想是，任何时刻证券的价格都完全并正确地反映了所有可获取的信息。换言之，市场的价格波动，取决于投资者的对未来收益率的预期。市场有效性的基本假设是证券存在一个客观的均衡价值，其价格已反映所有已知的信息，并且总是趋于均衡价值。这一假设意味着市场中的投资者是理性的经济人，其买卖的理性决策行为将使证券的价格趋向其内在价值，而价格趋向均衡的速度依赖于信息的可利用性和市场的竞争性。

　　在弱式有效市场中，价格的变化无法通过历史收益率进行预测，即价格变动是随机的，因此对弱式有效市场的检验主要侧重于检验收益率时间序列是否存在自相关性，或长期记忆性，其中最常用的是随机游走模型。技术交易者的一个基本理念是，历史总是不断重复的，价格时间序列中存在各种各样的价格模式，只要识别出这些模式，就可能战胜市场获取超额利润。而在弱式有效的市场中，价格波动不具记忆性。随机游走模型可追溯到1900年Bachelier的工作，1933年Cowles三世开始了早期实证研究，而Samuelson在1967年的论文则明确指出价格波动是随机的。

　　1970年，Mandelbrot提出用R/S分析研究证券收益率，认为价格时间序列具有长程相关性u引心1。1991年，Lo给出了修正R/S分析，用于对R/S分析的结果进行统计检验，并指出许多霍斯特指数大于0.5的价格时间序列的长期记忆性并不显著，此后的实证研究大多支持Lo的结论。1999年，Teverovsky等人指出，Lo的修正R/S分析倾向于过度拒绝长期记忆性，然而这一研究并未受到研究者的应有重视。

　　三、多重分形特性

　　最早用多重分形理论分析金融时问序列的学者可能是Ghashghme等人，他们将外汇市场与湍流类比，发现美元和德国马克外汇价格波动的矩函数具有非线性的标度律，而其他关于汇市多重分形特性的实证研究也得到了广泛关注。多重分形特性在其他金融时间序列中也有大量报道，如黄金价格、商品价格、股票个股价格、股市指数等。在大量实证研究报道金融市场价格序列的多重分形特性的同时，也出现了不少多重分形模型用来描述这个特性。

　　然而，大部分文献只热衷于报道实证研究的结果，却忽略了更本质的内容，即产生多重分形特性的原因。研究表明，即使是一个不具多重分形特性的分形模型，也可能产生所谓的多重分形性质旧引。

　　因而这些实证得到的多重分形特性，更确切的表述应该是“经验多重分形特性”。时间序列中的经验多重分形特性有两个可能的来源，一是波动性中存在的长程相关性，二是收益率的胖尾分布曙利。对很多金融时间序列，经验多重分形特性源于胖尾分布的零假设无法拒绝口引，这一结论已经为一些研究所证实，而部分金融时间序列的多重分形谱具有很窄的奇异性分布，进一步为之提供了佐证。这些问题指出，需要用更坚实有效的方法更深入地研究金融市场中的多重分形特性。

　　四、金融市场的微观模型

　　为了理解金融市场交易者行为对形成市场宏观规律影响，可以构建并研究各种不同的微观模型。模型市场的基本元素是经纪人，市场运行的规则既可以是基于经纪人的局部相关作用，也可以是受全局因素影响，或者是两者的叠加，这些模型能够产生部分程式化性质。对于部分程式化规律可能存在争议，但对微观模型而言，如果得到的价格时间序列具有与实际时间序列相同的程式化规律，则可认为该微观模型在某些方面抓住了实际市场的属性。基于经纪人的微观模型主要包括四类：

　　第一类，基本面交易者和噪声交易者博弈。根据交易定价策略的不同，金融市场中的交易者大致可以分为两类，一部分交易者属于基本面分析学派，认为资产股票的实际价格在偏离基础价格后必然将回复到基础价格，而另一部分交易者则信奉技术分析，属于技术分析交易者或图形交易者，他们通过对价格走势和模式的分析来确定投资策略。在微观市场模型的研究中，噪声交易者通常用来指称技术分析者，在所构建的模型市场中，基本面交易者和噪声交易者相互转化，从而形成市场价格。1997年Bak等人提出的扩散反应模型晗鲫和1999年提出的Lux-Marchesi模型即属于此类。

　　第二类，逾渗模型。这类模型最早由Cont和Bouchaud提出(CB模型)，认为羊群行为是收益率胖尾分布的微观机理。该模型不考虑外界因素对交易者的影响，交易者之间通过局部相互影响，产生一个个簇，每个簇内的交易者采取相同的交易策略。Stauffer发现，CB模型属于高维逾渗模型，是静态的。Eguiluz和Zimmermann提出的EZ模型，是CB模型的一个动态推广，通过信息传播和羊群效应产生与CB模型一致的幂律尾分布，抛弃了CB模型需要在临界点附近演化的人为规定。EZ模型及其部分衍生模型可写出演化方程并求解。

　　第三类，自旋模型。其中，伊辛模型中的经纪人具有买和卖两种状态，而帕兹模型则包含买、卖和观望三种状态。

　　第四类，少数者博弈模型。在各种微观模型，最引人注目并被广泛研究的模型，当数Challet和Zhang在1997年提出的少数者博弈模型，该模型基于Arthur提出的“酒吧问题”，用来描述适应经纪人对有限资源的竞争，其中的少数者获胜。

　　五、金融市场的宏观模型

　　对数周期性幂律模型是基于交易者之间的相互模仿，这些局部相互作用可形成正反馈，从而导致泡沫和反泡沫的产生，因此可用于金融泡沫和反泡沫的建模和预测。对数周期性幂律模型可分为两大类：维尔斯特拉斯族模型和朗道族模型，前者可以通过重整化群方法导出，而后者则是在临界点附近的各级朗道展开近似。

　　对数周期性幂律模型在股市中的应用，最早在1995年由两个小组独立提出，并在泡沫湮没时间预测和反泡沫走势预测方面取得了不少成功，如日本日经指数反泡沫、英国房地产泡沫、中国股市反泡沫等。

• 经济物理学