期望效用函数理论
出自 MBA智库百科(https://wiki.mbalib.com/)
期望效用函数理论（Expected Utility Theory），也称冯·纽曼--摩根斯坦效用函数（von Neumann-Morgenstern utility）
目录 |
期望效用函数理论是20世纪50年代,冯·纽曼和摩根斯坦(Von Neumann and Morgenstern)在公理化假设的基础上，运用逻辑和数学工具，建立了不确定条件下对理性人(rational actor)选择进行分析的框架。不过, 该理论是将个体和群体合而为一的。后来，阿罗和德布鲁（Arrow and Debreu）将其吸收进瓦尔拉斯均衡的框架中，成为处理不确定性决策问题的分析范式，进而构筑起现代微观经济学并由此展开的包括宏观、金融、计量等在内的宏伟而又优美的理论大厦。
如果某个随机变量X以概率Pi取值xi，i=1,2,…,n，而某人在确定地得到xi时的效用为u(xi)，那么，该随机变量给他的效用便是：
U(X) = E[u(X)] = P1u(x1) + P2u(x2) + ... + Pnu(xn)
其中，E[u(X)]表示关于随机变量X的期望效用。因此U(X)称为期望效用函数，又叫做冯·诺依曼—摩根斯坦效用函数（VNM函数）。另外，要说明的是期望效用函数失去了保序性，不具有序数性。
期望效用函数理论分析[1]
考虑两人的博弈(两人零和博弈)，二者出同样多的钱(100元)赌博，赢者变成200元，输者为0。不考虑其他因素情况下，输赢概率均为0.5，期望效用E(u)=0.5×200+0.5×0=100。双方的效用为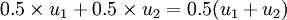
，u1,u2为两种状态下的边际效用(如上图)。比赌博前的u1少了
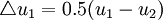。如果一个人拥有200元，再拿出100元进行赌博，其损失效用为
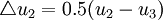，比较
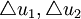如下：
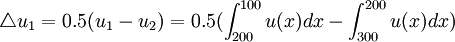
对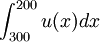
作变量替换t=x-100，得
,
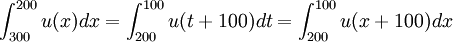![\triangle u_1=0.5\int_{200}^{100}[u(x)-u(x+100)]dx=0.5\int_{200}^{100}-u^{\prime}(\mu_1)100dx=-0.5u^{\prime}(\mu_1)100^2,\mu\in(100,300)](/w/images/math/5/1/a/51a084d01079715125ca370898dc3078.png)
![\triangle u_2=0.5(\int_{300}^{200}u(x)dx-\int_{400}^{300}u(x)dx)=0.5\int_{200}^{100}u(x+100)dx-\int_{200}^{100}u(x+200)dx=0.5\int_{200}^{100}u[(x+100)-u(x+200)]dx=-0.5u^{\prime}(\mu_2)100^2,](/w/images/math/8/1/f/81f6a1fa57915d5b5ae56538b4ebdbeb.png)
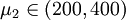且100 < μ1 < μ2 < 400,
![\triangle u_2-\triangle u_1=[u^{\prime}(\mu_1)-u^{\prime}(\mu_2)]100^2=\frac{1}{2}u^{\prime\prime}(\mu)100^2,100^2<\mu<400.](/w/images/math/0/3/e/03e5c544177b0ece991ea7230f5820b7.png)
当u为凹函数时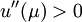
，当u是凸函数时
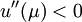，当u是直线时，
。所以当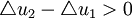
时，u为凸函数；
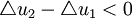时，u为凹函数；
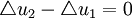时，u为直线。
由此可见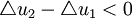，时，即一个富人拿出一部分钱去赌博所损失的效用要低于一个穷人拿出同样的钱去赌博所损失的效用。也就是说富人更经得起这种赌博带来的效用损失。因而u是凹函数。
EU理论及SEU理论描述了“理性人”在风险条件下的决策行为。但实际上人并不是纯粹的理性人，决策还受到人的复杂的心理机制的影响。因此，ＥＵ理论对人的风险决策的描述性效度一直受到怀疑。例如，EU理论难以解释阿莱悖论、Ellsberg悖论等现象；没有考虑现实生活中个体效用的模糊性、主观概率的模糊性；不能解释偏好的不一致性、非传递性、不可代换性、“偏好反转现象”、观察到的保险和赌博行为；现实生活中也有对EU理论中理性选择上的优势原则和无差异原则的违背；实际生活中的决策者对效用函数的估计也违背EU理论的效用函数。
另外，随着实验心理学的发展，预期效用理论在实验经济学的一系列选择实验中受到了一些“悖论”的挑战。实验经济学在风险决策领域所进行的实验研究最广泛采取的是彩票选择实验（lottery－choice experiments），即实验者根据一定的实验目标，在一些配对的组合中进行选择，这些配对的选择通常在收益值及赢得收益值的概率方面存在关联。通过实验经济学的论证，同结果效应、同比率效应、反射效应、概率性保险、孤立效应、偏好反转等“悖论”的提出对预期效用理论形成了重大冲击。
研究者针对以上问题提出了以下几种使EU理论一般化的方式:
(1)Karmark(1978)提出主观权重效用(Subjectively Weighted Utility，SWU)的概念，用决策权重替代线性概率，这可以解释Allais问题和共同比率效应，但不能解释优势原则的违背；
(2)扩展性效用模型（generalized utility model）。该类模型的特点是针对同结果效应和同比率效应等，放松预期效用函数的线性特征，或对公理化假设进行重新表述，模型将用概率三角形表示的预期效用函数线性特征的无差异曲线，扩展成体现局部线性近似的扇行展开。这些模型没有给出度量效用的原则，但给出了效用函数的许多限定条件。
(3)Kahneman和阿莫斯·特沃斯基（Amos Tversky）(1979)引入系统的非传递性和不连续性的概念，以解决优势违背问题；
(4)“后悔”的概念被引入，以解释共同比率效应和偏好的非传递性；如Loomes和Sudgen（1982）所提出的“后悔模型”引入了一种后悔函数，将效用奠定在个体对过去“不选择”结果的心理体验上（放弃选择后出现不佳结果感到庆幸，放弃选择后出现更佳结果感到后悔），对预期效用函数进行了改写（仍然保持了线性特征）。
(5)允许决策权重随得益的等级和迹象变化，这是对SWU的进一步发展。
(6)非可加性效用模型（non-additivity utility model）这类模型主要针对埃尔斯伯格悖论，该模型认为概率在其测量上是不可加的。
风险的主观态度[2]
1．风险偏好
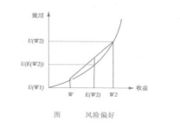
风险偏好表明经济代理人对于风险的个人偏好状态，其效用随资金报酬的增加而增加，增加率递增。无论人们对风险承担者的概念作何种理解，我们都可以肯定地认为，获取随机报酬形比获取确定报酬W=E[W]所承担的风险要大得多。如果某个市场参加者总是宁愿获取W=E[W]的报酬(相应获得U(E[W])的效用)，而且他也愿意承担风险获取风险报酬W(相应获得的预期效用为E(U[W]))，那么，我们就称这个市场参加者为风险偏好者。也就是说，当面临多种同样资金预期值的投机方式时，风险偏好者将选择具有较大不确定性的投机方式。U(E[X])<E(U[X])，风险偏好的效用函数是凸函数。如图所示，效用的增加率随报酬的增加而递增。效用函数的二阶导数大于零。
2．风险中性
风险中性是相对于风险偏好和风险厌恶的概念，风险中性的投资者对自己承担的风险并不要求风险补偿。我们把每个人都是风险中性的世界称之为风险中性世界，这样的世界里，投资者对风险不要补偿，所有证券的期望报酬率都是无风险利率。真实世界里的投资者尽管在风险偏好方面存在差异，但当套利机会出现时，投资者无论风险偏好如何都会采取套利行为，消除套利机会后的均衡价格与投资者的风险偏好无关。风险中性者并不介意一项投机是否具有比较确定或者不那么确定的结果。他们只是根据预期的资金价值来选择投机，特别而言，他们要使期望资金价值最大化。下图效用的增加率不随报酬的增加而变动，效用函数的二阶导数等于零。U=a+bM，其中U为效用，M为资金报酬，a和b是常数(b>0)。U(E[X])=E(U[X])风险中性的效用函数是条直线。
3．风险厌恶
风险厌恶是一个人接受一个有不确定的报酬的交易时，相对于接受另外一个更保险，但是也可能具有更低期望报酬的交易的不情愿程度。风险厌恶是一个人在承受风险情况下其偏好的特征，可以用它来测量人们为降低所面临的风险而进行支付的意愿。在降低风险的成本与报酬的权衡过程中，厌恶风险的人们在相同的成本下更倾向于做出低风险的选择。例如，如果通常情况下你情愿在一项投资上接受一个较低的预期回报率，因为这一回报率具有更高的可测性，你就是风险厌恶者。当对具有相同的预期回报率的投资项目进行选择时，风险厌恶者一般选择风险最低的项目。当面对具有相同预期资金价值的投机时，风险厌恶者喜欢结果比较确定的投机，而不喜欢结果不那么确定的投机。在信息经济学中，风险厌恶者的效用函数一般被假设为凹性。如图所示，效用上网增加率随报酬的增加递减。效用函数的二阶导数小于零，U(E[X])>E(U[x])风险厌恶的效用函数是凹函数。
CE 被称作确定性等值(Certainty. Equivalent)，即消费者为达到期望的效用水平所要求保证的财产水平。若某人的财富效用函数为u(x)，而一个赌局对某人的效用为E(u(x))，则有一个CE值能够满足：u(CE)=E(u(x))。称CE为某人在该赌局中的确定性等值。
保险市场的价格——保险金：若某人的财富数量为w，其财富效用函数为u(x)，而一个赌局对某人的效用为u(E(x))，若有u(w-R)= u(E(x))，则称R为保险金。因为u(w-R)= u(CE)，所以R=w-CE。
风险厌恶者是保险的需求者，同时也可以成为保险的供给者。
案例一:期望效用函数理论在就业管理中的应用[3]
一、就业期望效用函数的构造
从不确定性出发，考虑人们的偏好与效用函数就得引进概率P。概率的效用函数表达式叫期望效用函数，如果把期望效用函数与大学生择业、就业结合就可以较简单地构造出就业期望效用函数探讨大学生就业的现象机制一般来讲是在条件确定时进行的经验或者理性的推导。但是，许多场合，那种以完全确定为前提的分析是不现实的。事实上，我们知道，毕业生在决策时，对于选择的后果是不完全知道的，具有不确定性，要冒一定的风险。
毕业生的决策是取决于他(她)关于选择某一个工作岗位的概率分布的主观猜测。如果他主观认为选择某一工作发展前景概率更高，那么，它就会选择，否则另谋出路。这就是我们必须从不确定性出发，考虑消费者的偏好与效用函数就得引进概率P使之变成期望效用函数。如果你选择的工作对象是两家IT公司，收入见下表。
表工资收入。
| 结果1 | 结果2 | |||
| 可能性(P) | 收入 | 可能性(P) | 收入 | |
| 工作A:(佣金制) | 0.6 | 2000 | 0.4 | 1000 |
| 工作B:(固定资金) | 0.95 | 1500 | 0.05 | 500 |
期望收入=(结果1的概率)×(结果1的收入)+(结果2的概率)×(结果2的收入)。工作A=1600。工作B=1450则你应该选择工作A，而期望效用(expected utility)一般在单赌的情况下值为u(g)=pu(A)+(1-P)u(B)当u(g1) > u(g2)时，则可认为毕业时在g_1与g_2之间更偏好g_1。也就是说，当寻找工作的毕业生有多种未知的情况，而要选择时，他们能够依靠期望效用的极大化来代表分析自己的主观选择。如果选择工作的结果有，n个可能性，即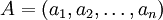
，同时对u(ai)(i=1,2,……,n)赋值，代人构造的就业期望效用函数。如果
即对毕业生来说，ai最好，an最次。如果学生把ai看成是a1与an的一个线性组合一样好，在他看来，任一个可能结果ai(i=1,2,……,n)总不外是与最好的结果与最次的结果之间的某种组合一样好，即ai～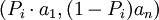
令u(ai) − = pi即用毕业生心里那个使a与某个单赌等价的最好事件发生概率P_i来定义u(a_i)则可构建就是期望效用函数为：。
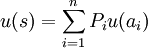就业期望效用函数的意义在于，当大学生面临不确定性的择业、就业选择时，他可以依靠期望效用的极大化来分析自己的选择是否合理可行，至少可以对目前的状况做较规范的分析。
二、效用函数应用实例
假设目前市场上由三份工作可以选择，它们的工资分别为A=(3000元，1500元，1000元)括号中的a1 = 3000,a2 = 1500,a3 = 1000，分别表示可能发生的三种结果，这里a1最好，a3最次。
如果问自己：当a发生的概率(p)等于多少时使你认为a(i=1，2，3)与(p,a1,a2)元差异?如果回答是：3000元～(1×(3000元)，0×(1000元)，1500元～(0.6×(3000元)，0.4×(1000元))，1000元～(0×(3000元)，1×(1000元))那么可以定义：
u=(3000元) = u(a1) = 1
u=(1500元) = u(a2) = O.6
u=(1000元)=u = (a3) = O
现在可以比较不同寻职格局了。比如：
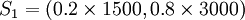
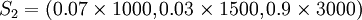
则u(S1) = 0.2u(1500) + 0.8u(3000) = 0.92
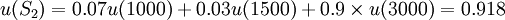
由于u(S1) > u(S2)即S1的期望效用大于S2的期望效用，所以你=定会偏好于选择S1。因此就业者可以通过自己对某=行业的了解及心理自测的评价，利用就业期望效益较合理评估自己的想法，寻找更多的机会和更合适的工作岗位。
本条目由以下用户参与贡献
Lolo,funwmy,沙漠之鹰,Wwdz,Vulture,山林,Zfj3000,Franklee0415,Cabbage,Jacksonzl,Smileandblue,Zjjsljt,Angle Roh,Dan,Yixi,HEHE林,泡芙小姐,林巧玲,LuyinT,刘维燎.评论(共34条)
图1 和图2 反了
没有吧~ 我看是没错~ 不知道别人有没有什么高见~
没错啊
确定性等值能补充一个具体例子吗？
添加了新的案例，希望对您有帮助！
很牛，就是不详细啊！！，看看西方经济学教材，理解一下
添加了新内容，希望对您有帮助！
其中，E[u(X)]表示关于随机变量X的期望效用。因此U(X)称为期望效用函数，又叫做冯·诺依曼—摩根斯坦效用函数（VNM函数）。
关于这句话，我很不解，因为课上，我们老师说，u(x)是vNM函数，而不是U（x）。 所以我很困惑，自己想着觉得是U（x）,而不是u(x),因为这样比较有逻辑，不是么？ 但是为什么跟我们老师说的不一样呢？？？？
求解答。 谢谢。
比赌博前的u1少了......。如果一个人拥有200元，再拿出100元进行赌博，其损失效用为..... 1，为什么说是比u1少了呢？钱多了，不是效用高了么？ 不是比u1增多了么？为什么图是减函数呢？不是应该是增函数么？ 2，为什么说是损失效用呢？ 3，关于定积分的计算，为什么下限值比上限值高呢？为什么不是反过来呢？ 4，关于定积分的计算，我不会算。。。。请大家指教，，，，不要因为太简单而忽略我的问题拜托。。。。
由此可见，时，即一个富人拿出一部分钱去赌博所损失的效用要低于一个穷人拿出同样的钱去赌博所损失的效用。也就是说富人更经得起这种赌博带来的效用损失。因而u是凹函数。 我觉得这个“因而u是凹函数。” 的逻辑怪怪的。为什么从其中一个情况，就可以推出整个u函数都是凹函数呢？
还有，关于对期望效用函数的介绍，似乎不是很。。很什么来着（我想不到词。。）。。。换句话说，在课上，跟我们老师所介绍的不一样，我们老师介绍的是，vnm的定理和性质。我想，这样介绍会不会更清晰明了一些，比如，vnm 是假设它本身就是线性增函数的。 这样的话，就不会出现“因而u是凹函数。”的困惑了。 不知道大家怎么看？
我连图2都没看到…… 但我也觉得图1不对，vnm应该是增函数呀，怎么变减函数了？？？？？？
其实看到这里我已经完全米糊了。。。。按上面的计算，图是对的，可是，vnm就是增函数不是么？？而且应该是线性的呀？？？
若某人的财富数量为w，其财富效用函数为u(x)，而一个赌局对某人的效用为u(E(x))。 我不明白的是， 前面说 其财富效用函数为u(x)， 而一个赌局对某人的效用为u(E(x))。为什么效用变成了 u(E(x))？？？？ 同样是效用，为什么表达方式不一样，或者说用另一个词，比如偏好，还是什么的。额。。。说来说去，我不明白的就是，效用这个词，为什么用两个不用的函数表示？
当a发生的概率(p)等于多少时使你认为a(i=1，2，3)与(p,a1,a2)元差异?如果回答是：3000元～(1×(3000元)，0×(1000元)，1500元～(0.6×(3000元)，0.4×(1000元))，1000元～(0×(3000元)，1×(1000元))那么可以定义。。。。 1500那个，括号里的数，不是比1500多了么？
图1 和图2 反了 +1
图应该是对的，现更新了原文的内容，添加了文献出处，希望对您有帮助！~
lz，风险偏好和风险厌恶的公式反了，请查阅相关书籍，如Claus Munk的Dynamic Asset Allocation.
lz，风险偏好和风险厌恶的公式反了，请查阅相关书籍，如Claus Munk的Dynamic Asset Allocation.
谢谢您的指正，原文已修正！~
MBA智库百科是可以自由参与的百科，如有发现错误和不足，您也可以参与修改编辑，只要通过网页右上角的创建新帐号，创建用户名后即可参与，期待您的加入哦！~
不是直接相乘，应该理解成U(1500)~(0.6U(3000),0.4U(1000))
由此可见，时，即一个富人拿出一部分钱去赌博所损失的效用要低于一个穷人拿出同样的钱去赌博所损失的效用。也就是说富人更经得起这种赌博带来的效用损失。因而u是凹函数。 我觉得这个“因而u是凹函数。” 的逻辑怪怪的。为什么从其中一个情况，就可以推出整个u函数都是凹函数呢？
还有，关于对期望效用函数的介绍，似乎不是很。。很什么来着（我想不到词。。）。。。换句话说，在课上，跟我们老师所介绍的不一样，我们老师介绍的是，vnm的定理和性质。我想，这样介绍会不会更清晰明了一些，比如，vnm 是假设它本身就是线性增函数的。 这样的话，就不会出现“因而u是凹函数。”的困惑了。 不知道大家怎么看？
赌博问题，双方0.5概率，当u1无限接近u2的时候就是最低，当u1大于u2就是上升，是凹函数
赌博问题，双方0.5概率，当u1无限接近u2的时候就是最低，当u1大于u2就是上升，是凹函数
他证明得知u的函数是小于零 、
看不懂啊。。。