策略（博弈论）

出自 MBA智库百科(https://wiki.mbalib.com/)

　　在博弈论里，策略是指在所有可能发生情况下的一套完整行动计划；这完全决定了玩家的行为。玩家的策略会决定玩家在赛局的任一阶段所采取的行动，不论这一阶段之前是如何演变而来的。

　　策略组合是每个玩家都完全选定他们在赛局中所有行动的一套策略。一个策略组合对每个玩家都必须包括一个且只能一个的策略。策略有时会和移动搞混。移动是指玩家在赛局中某一点所采取的行动；策略则是完整的算法，告诉玩家在赛局中的每一个可能情况下要如何动作。

　　策略集合是个由玩家所能采取的策略所组成的集合。

　　若玩家有有限个具体的策略可供选择，则称其有个有限策略集合。例如，在单一次剪刀、石头、布里，每一个玩家都有一个有限策略集合 {剪刀, 石头, 布} 。若有无限个具体的策略可供选择，则称其有个无限策略集合。例如，有规范出价增额的拍卖会有个无限策略集合 {$10, $20, $30, ...} 。另外，在分蛋糕问题里则有个连续的策略集合 {在蛋糕的百分之零至百分之百间的任一处切分} 。

　　在动态赛局里，策略集合是由玩家能够给定机器人如何进行赛局的规则所组成的。例如，在最后通牒赛局里，第二位玩家的策略集合应该是由要接受及要拒绝的各种规则所组成的。在贝叶斯博弈里，其策略集合和动态赛局的相似，由任何私有情报所会采取的行动规则所组成。

　　在应用赛局理论里，策略集合的定义是使赛局能同时可解及有意义的重要一部分；利用对整个问题的了解来限制策略空间，以简化问题。例如，严格来说，在最后通牒赛局里，玩家可以有策略如下：“拒绝 ($1, $3, $5, ..., $19)，而接受 ($0, $2, $4, ...,$20) ”。包括所有的策略会使得策略空间变得很大，并且得到一个稍难的问题；但对这赛局的理解，相信是可以限制其策略集合为 {拒绝所有不大于x的钱，而接受所有大于x的钱；这里的x等于 ($0, $1, $2, ..., $20) 的其中一个} 。

　　策略集合是由玩家能够施行的纯策略所组成的集合。例如“剪刀、石头、布”中，玩家只有剪刀、石头和布这三个策略。纯策略就是只使用策略集合中其中一条策略。

　　混合策略是对每个纯策略分配一个概率而形容的策略。混合策略允许玩家随机选择一个纯策略。因为概率是连续的，所以即使策略集合是有限的，也会有无限多个混合策略。 当然，严格来说，每个纯策略都是一个“退化”的混合策略，某一特定纯策略的概率为1，其他的则为0。

　　完全混合策略是个混合策略，其对每个纯策略都分配了一个不为零的概率。（完全混合策略对如颤手完全均衡之类的均衡精细很重要。）

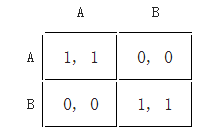
　　假设一收益矩阵表示如下（为一协调赛局）。这里，一个玩家选择列（Column），另一个玩家选择行(Row)。列玩家得到第一个收益，行玩家则得到第二个。若列玩家偏向百分之百选择A，则称他在玩纯策略。若行玩家偏向以掷硬币来决定，若头朝上则选择A，若字朝上则选择B，则称他在玩混合策略，而非纯策略。