策略(博弈論)
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
在博弈論里,策略是指在所有可能發生情況下的一套完整行動計劃;這完全決定了玩家的行為。玩家的策略會決定玩家在賽局的任一階段所採取的行動,不論這一階段之前是如何演變而來的。
策略組合是每個玩家都完全選定他們在賽局中所有行動的一套策略。一個策略組合對每個玩家都必須包括一個且只能一個的策略。策略有時會和移動搞混。移動是指玩家在賽局中某一點所採取的行動;策略則是完整的演算法,告訴玩家在賽局中的每一個可能情況下要如何動作。
策略集合是個由玩家所能採取的策略所組成的集合。
若玩家有有限個具體的策略可供選擇,則稱其有個有限策略集合。例如,在單一次剪刀、石頭、布里,每一個玩家都有一個有限策略集合 {剪刀, 石頭, 布} 。若有無限個具體的策略可供選擇,則稱其有個無限策略集合。例如,有規範出價增額的拍賣會有個無限策略集合 {$10, $20, $30, ...} 。另外,在分蛋糕問題里則有個連續的策略集合 {在蛋糕的百分之零至百分之百間的任一處切分} 。
在動態賽局里,策略集合是由玩家能夠給定機器人如何進行賽局的規則所組成的。例如,在最後通牒賽局里,第二位玩家的策略集合應該是由要接受及要拒絕的各種規則所組成的。在貝葉斯博弈里,其策略集合和動態賽局的相似,由任何私有情報所會採取的行動規則所組成。
在應用賽局理論里,策略集合的定義是使賽局能同時可解及有意義的重要一部分;利用對整個問題的瞭解來限制策略空間,以簡化問題。例如,嚴格來說,在最後通牒賽局裡,玩家可以有策略如下:“拒絕 ($1, $3, $5, ..., $19),而接受 ($0, $2, $4, ...,$20) ”。包括所有的策略會使得策略空間變得很大,並且得到一個稍難的問題;但對這賽局的理解,相信是可以限制其策略集合為 {拒絕所有不大於x的錢,而接受所有大於x的錢;這裡的x等於 ($0, $1, $2, ..., $20) 的其中一個} 。
策略集合是由玩家能夠施行的純策略所組成的集合。例如“剪刀、石頭、布”中,玩家只有剪刀、石頭和布這三個策略。純策略就是只使用策略集合中其中一條策略。
混合策略是對每個純策略分配一個概率而形容的策略。混合策略允許玩家隨機選擇一個純策略。因為概率是連續的,所以即使策略集合是有限的,也會有無限多個混合策略。 當然,嚴格來說,每個純策略都是一個“退化”的混合策略,某一特定純策略的概率為1,其他的則為0。
完全混合策略是個混合策略,其對每個純策略都分配了一個不為零的概率。(完全混合策略對如顫手完全均衡之類的均衡精細很重要。)
假設一收益矩陣表示如下(為一協調賽局)。這裡,一個玩家選擇列(Column),另一個玩家選擇行(Row)。列玩家得到第一個收益,行玩家則得到第二個。若列玩家偏向百分之百選擇A,則稱他在玩純策略。若行玩家偏向以擲硬幣來決定,若頭朝上則選擇A,若字朝上則選擇B,則稱他在玩混合策略,而非純策略。
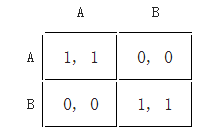








列不應是column嗎 行才是row吧