最优所得税理论
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
最优所得税理论旨在分析和解决所得课税在公平与效率之间的权衡取舍问题。
谈及所得税问题,我们立即面临有名的“做蛋糕”与“切蛋糕”之间的权衡问题。
一种观点认为,所得税是为满足公平目标而有效实施再分配的手段;
另一种观点认为,所得税的课征是对劳动供给和企业精神的一种主要抑制因素,特别是当边际税率随着所得的增加而增加的时候。最优所得税理论旨在分析和解决所得课税在公平与效率之间的权衡取舍问题。
最优所得税理论的内容[1]
关于最优所得税的主要论文出自米尔利斯(Mirrlees,1971),他研究了非线性所得税的最优化问题。米尔利斯模型在所得税分析中的价值在于它以特定方式抓住了税制设计问题的性质。
首先,为了在税收中引入公平因素,米尔利斯设想无税状态下的经济均衡具有一种不公平的所得分配。所得分配由模型内生而成,同时每个家庭获取的所得各不相同。
其次,为了引进效率方面的考虑,所得税必须影响家庭的劳动供给决策。此外,经济要具有充分灵活性,以便不对可能成为问题答案的税收函数施加任何事先的约束。米尔利斯的模型是集合上述要素的一种最为简单的描述。
米尔利斯模型得出的重要的一般结果是:
(1)边际税率应在0与1之间;
(2)有最高所得的个人的边际税率为0;
(3)如果具有最低所得的个人按最优状态工作,则他们面临的边际税率应当为0.毫无疑问,第二点结论是最令人感到惊奇的。
不过,这一结论的重要性也许不在于告诉政府应该通过削减所得税表中最高所得部分的税率,以减少对最高收入者的作用;其重要性更在于它表明最优税收函数不可能是累进性的,这就促使人们必须重新审视利用累进所得税制来实现再分配的观念。也许说,要使得关注低收入者的社会福利函数最大化,未必需要通过对高收入者课重税才能实现,事实上,让高收入承担过重的税负,其结果可能反而使低收入者的福利水平下降。
由于米尔利斯的非线性模型在分析上十分复杂,其结论也只是提供给我们关于政策讨论的指导性原则。为了得到最优税收结构的更详细情况,有必要考察数值方面的分析。米尔利斯根据他所建立的模型,计算出完整的最优所得税率表。从结果看,高所得的边际税率的确变得很低,但并未达到0.同时低所得的平均税率均为负,从而低收入者可以从政府那里获得补助。托马拉(Tuomala,1990)所做的数值分析则进一步表明,接近最高所得的边际税率可能远不是0,这意味着最高所得的边际税率为零的结果只是一个局部结论。从政策目的上看,基于米尔利斯模型所得出的重要结论有:
(1)最优税收结构近似于线性,即边际税率不变,所得低于免税水平的人可获得政府的补助。
(2)边际税率相当低。
(3)所得税实际上并非一个缩小不平等的有效工具。
斯特恩(Stern,1976)根据一些不同的劳动供给函数、财政收入的需要和公平观点,提出了最优线性所得税模型。他得出的结论是,线性所得税的最优边际税率随着闲暇和商品之间的替代弹性的减小而增加,随着财政收入的需要和更加公平的评价而增加。这意味着,人们对减少分配不平等的关注越大,则有关的税率就应越高,这一点是与我们的直觉相符的。另一方面,最优税率与劳动供给的反应灵敏度、财政收入的需要和收入分配的价值判断密切相关,假如我们能够计算或者确定这些参数值,我们就可以计算出最优税率。因此,斯特恩模型对最优所得税制的设计具有指导意义。
最优所得税设计[2]
最优所得税与最优商品税不同,它是从讨论公平开始的,试图将公平考虑纳入最优税制的设计中来。最优所得税分最优个人所得税和最优企业所得税。
一.最优个人所得税
最优个人所得税常用斯特恩模型(Stern Model)进行分析:
斯特恩假定对一个人课征的税收收入用公式表示为:
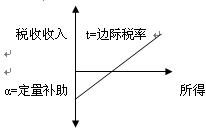
税收收入=-a+t×所得,其中a和t为正数。
公式可以用图表示。图中,所得用横轴表示,税收收入用纵轴表示,当所得为零时,个人的“税收负担”是负的,即他从政府取得a元的定量补助。而后,对每一元所得,个人必须向政府缴纳t元。这样,t是边际税率,即增加一元必须缴纳的比例。因为是一条直线表示,所以叫线性所得税曲线。
斯特恩模型包含的政策含义如下:
1.即使线性所得税曲线的边际税率不变,但个人所得税占所得的比例越高(税收收入/所得=-a/所得+t),即所得越高,就要以更高的比例缴纳税,因而线性所得税是累进的,即体现了纵向公平。
2.社会保障支出被当作负所得税与所得税结合使用,政府可以通过调整a和t的精确值来协调不同收入人群的负担率。
3.更大的t值是与更强的累进性税率相联系的,但在较大t值而导致更强累进性的同时,它们也造成了更大的超额负担。
4.在其他情况相同时,劳动力的供给越具有弹性,最优t值就应越小。再分配的“成本”是由税率t所造成的超额负担,劳动力供给越具有弹性,对其征税的超额负担就越大,为降低再分配的成本,我们对具有高弹性的劳动力供给尽量课以低税。
二.最优企业所得税
我们运用乔根森(Jorgenson)的新兴古典(New Classical)投资模型来讨论最优所得税设计问题。乔根森的新兴古典投资模型表示为:
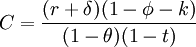
其中,C是使用者成本,r是税后利率,φ是经济折旧率,θ是企业所得税率,t是个人所得税率, k是投资的税收抵免,δ是每一元的折旧准许的现值,只要企业所得税制的变化影响与k的结合,资本的使用者成本就会变化。
企业所得税会提高使用者成本,而投资税收抵免与折旧准许则会降低使用者成本。我国现行的企业所得税实行内外资两套税制,由于税前列支标准和税收优惠不同,使得实际税负差别很大。根据税收的横向公平和WTO关于企业的国民待遇准则,统一内外资企业所得税税率(φ),税收抵免(k),制定一个同时适用内外资企业的所得税法势在必行。