多元线性回归分析预测法
出自 MBA智库百科(https://wiki.mbalib.com/)
多元线性回归分析预测法(Multi factor line regression method,多元线性回归分析法)
目录 |
在市场的经济活动中,经常会遇到某一市场现象的发展和变化取决于几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况。而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。例如,某一商品的销售量既与人口的增长变化有关,也与商品价格变化有关。这时采用一元回归分析预测法进行预测是难以奏效的,需要采用多元回归分析预测法。
多元回归分析预测法,是指通过对两个或两个以上的自变量与一个因变量的相关分析,建立预测模型进行预测的方法。当自变量与因变量之间存在线性关系时,称为多元线性回归分析。
多元线性回归的计算模型[1]
一元线性回归是一个主要影响因素作为自变量来解释因变量的变化,在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元线性回归。
设y为因变量,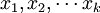 为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
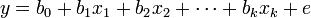
其中,b0为常数项,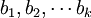 为回归系数,b1为
为回归系数,b1为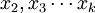 固定时,x1每增加一个单位对y的效应,即x1对y的偏回归系数;同理b2为x1,xk固定时,x2每增加一个单位对y的效应,即,x2对y的偏回归系数,等等。如果两个自变量x1,x2同一个因变量y呈线性相关时,可用二元线性回归模型描述为:
固定时,x1每增加一个单位对y的效应,即x1对y的偏回归系数;同理b2为x1,xk固定时,x2每增加一个单位对y的效应,即,x2对y的偏回归系数,等等。如果两个自变量x1,x2同一个因变量y呈线性相关时,可用二元线性回归模型描述为:
y = b0 + b1x1 + b2x2 + e
建立多元性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变量的选择,其准则是:
(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;
(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;
(3)自变量之间具有一定的互斥性,即自变量之间的相关程度不应高于自变量与因变量之间的相关程度;
(4)自变量应具有完整的统计数据,其预测值容易确定。
多元性回归模型的参数估计,同一元线性回归方程一样,也是在要求误差平方和(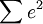 )为最小的前提下,用最小二乘法求解参数。以二线性回归模型为例,求解回归参数的标准方程组为:
)为最小的前提下,用最小二乘法求解参数。以二线性回归模型为例,求解回归参数的标准方程组为:

解此方程可求得b0,b1,b2的数值。亦可用下列矩阵法求得
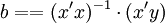
即

多元线性回归模型的检验[1]
多元性回归模型与一元线性回归模型一样,在得到参数的最小二乘法的估计值之后,也需要进行必要的检验与评价,以决定模型是否可以应用。
1、拟合程度的测定。
与一元线性回归中可决系数r2相对应,多元线性回归中也有多重可决系数r2,它是在因变量的总变化中,由回归方程解释的变动(回归平方和)所占的比重,R2越大,回归方各对样本数据点拟合的程度越强,所有自变量与因变量的关系越密切。计算公式为:
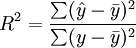
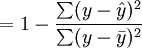
其中,
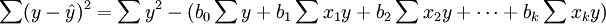
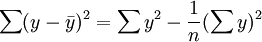
2.估计标准误差
估计标准误差,即因变量y的实际值与回归方程求出的估计值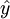 之间的标准误差,估计标准误差越小,回归方程拟合程度越强。
之间的标准误差,估计标准误差越小,回归方程拟合程度越强。
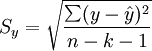

其中,k为多元线性回归方程中的自变量的个数。
3.回归方程的显著性检验
回归方程的显著性检验,即检验整个回归方程的显著性,或者说评价所有自变量与因变量的线性关系是否密切。常采用F检验,F统计量的计算公式为:
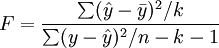
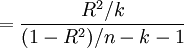
根据给定的显著水平a,自由度(k,n-k-1)查F分布表,得到相应的临界值Fa,若F > Fa,则回归方程具有显著意义,回归效果显著;F < Fa,则回归方程无显著意义,回归效果不显著。
4.回归系数的显著性检验
在一元线性回归中,回归系数显著性检验(t检验)与回归方程的显著性检验(F检验)是等价的,但在多元线性回归中,这个等价不成立。t检验是分别检验回归模型中各个回归系数是否具有显著性,以便使模型中只保留那些对因变量有显著影响的因素。检验时先计算统计量ti;然后根据给定的显著水平a,自由度n-k-1查t分布表,得临界值ta或ta / 2,t > t − a或ta / 2,则回归系数bi与0有显著差异,反之,则与0无显著差异。统计量t的计算公式为:
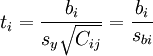
其中,Cij是多元线性回归方程中求解回归系数矩阵的逆矩阵(x'x) − 1的主对角线上的第j个元素。对二元线性回归而言,可用下列公式计算:
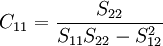
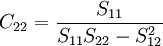
其中,
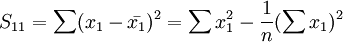
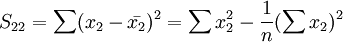
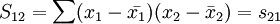
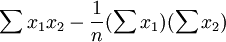
5.多重共线性判别
若某个回归系数的t检验通不过,可能是这个系数相对应的自变量对因变量的影响不显著所致,此时,应从回归模型中剔除这个自变量,重新建立更为简单的回归模型或更换自变量。也可能是自变量之间有共线性所致,此时应设法降低共线性的影响。
多重共线性是指在多元线性回归方程中,自变量之间有较强的线性关系,这种关系若超过了因变量与自变量的线性关系,则回归模型的稳定性受到破坏,回归系数估计不准确。需要指出的是,在多元回归模型中,多重共线性的难以避免的,只要多重共线性不太严重就行了。
判别多元线性回归方程是否存在严重的多重共线性,可分别计算每两个自变量之间的可决系数r2,若r2 > R2或接近于R2,则应设法降低多重线性的影响。亦可计算自变量间的相关系数矩阵的特征值的条件数k = λ1 / λp(λ1为最大特征值,λp为最小特征值),k<100,则不存在多重点共线性;若100≤k≤1000,则自变量间存在较强的多重共线性,若k>1000,则自变量间存在严重的多重共线性。降低多重共线性的办法主要是转换自变量的取值,如变绝对数为相对数或平均数,或者更换其他的自变量。
6.D.W检验
当回归模型是根据动态数据建立的,则误差项,若误差序列诸项之间相互独立,则误差序列各项之间没有相关关系,若误差序列之间存在密切的相关关系,则建立的回归模型就不能表述自变量与因变量之间的真实变动关系。D.W检验就是误差序列的自相关检验。检验的方法与一元线性回归相同。
案例一:公路客货运输量多元线性回归预测方法探讨[2]
一、背景
公路客、货运输量的定量预测,有助于促进了公路运输经营决策的科学化和现代化。
线性回归分析法是以相关性原理为基础的,相关性原理是预测学中的基本原理之一。由于公路客、货运输量受社会经济有关因素的综合影响。所以,多元线性回归预测首先是建立公路客、货运输量与其有关影响因素之间线性关系的数学模型。然后通过对各影响因素未来值的预测推算出公路客货运输量的预测值。
二、公路客、货运输量多元线性回归预测方法的实施步骤
1.影响因素的确定
影响公路客货运输量的因素很多,主要包括以下一些因素:
(1)客运量影响因素
人口增长量、国民生产总值、国民收入工农业总产值,基本建设投资额城乡居民储蓄额铁路和水运客运量等。
(2)货运量影响因素
人口货车保有量(包括拖拉机),国民生产总值,国民收入、工农业总产值,基本建设投资额,主要工农业产品产量、社会商品购买力、社会商品零售总额、铁路和水运货运量额。
上述影响因素仅是对一般而言,在针对具体研究对象时会有所增减。因此,在建立模型时只须列入重要的影响因素,对于非重要因素可不列入模型中。若疏漏了某些重要的影响因素,则会造成预测结果的失真。另外,影响因素太少会造成模型的敏感性太强。反之,若将非重要影响因素列入模型,则会增加计算工作量,使模型的建立复杂化并增大随机误差。
影响因素的选择是建立预测模型首要的关键环节,可采取定性和定量相结合的方法进行,影响因素的确定可以通过专家调查法,其目的是为了充分发挥专家的聪明才智和经验。
具体做法就是通过对长期从事该地区公路运输企业和运输管理部门的领导干部、专家、工作人员和行家进行调查。可通过组织召开座谈会,也可以通过采访,填写调查表等方法进行,从中选出主要影响因素为了避免影响因素确定的随意性,提高回归模型的精度和减少预测工作量,可通过查阅有关统计资料后,再对各影响因素进行相关度(或关联度)和共线性分析,从而再次筛选出最主要的影响因素,所谓相关度分析就是将各影响因素的时间序列与公路客货运量的时间序列做相关分析事先确定—个相关系数,对相关系数小的影响因素进行淘汰,关联度是灰色系统理论中反映事物发展变化过程中各因素之间的关联程度,可通过建空公路客、货运量与各影响影响因素之间关联系数矩阵,按一定的标准系数舍去关联度小的影响因素,所谓共线性是指某些影响因素之间存在着线性关系或接近于线性关系,由于公路运输经济自身的特点,影响公路客,货运输量的诸多因素之间总是存在着一定的相关性,持别是与国民经济有关的一些价值型指标。
我们研究的不是有无相关性问题而是共线性的程度,如果影响因素之间的共线性程度很高,首先会降低参数估计值的精度。其次在回归方程建立后的统计检验中导致舍去重要的影响因素或错误地接受无显著影响的因素,从而使整个预测工作失去实际意义。关于共线性程度的判定,可利用逐步分析估计法的数理统计理论编制计算机程序来实现。或者通过比较rij和R2的大小来判定。在预测学上,一般认为当rij > R2时,共线性是严重的,其含义是,多元线性回归方程中所含的任意两个自变量xi,xj之间的相关系数rij大于或等于该方程的样本可决系数R2时,说明自变量中存在着严重的共线性问题。
2.建立经验线性回归方程
利用最小二乘法原理寻求使误差平方和达到最小的经验线性回归方程:
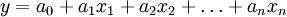
y——预测的客、货运量
g——各主要影响因数
3.数据整理
对收集的历年客、货运输量和各主要影响因素的统计资料进行审核和加工整理是为了保证预测工作的质量。
资料整理主要包括下列内容:
(1)资料的补缺和推算。
(2)对不可靠资料加以核实调整,对查明原因的异常值加以修正。
(3)对时间序列中不可比的资料加以调整和规范化;对按当年价格计算的价值指标应折算成按统。
4.多元线性回归模型的参数估计
在经验线性回归模型中,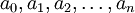 是要估计的参数,可通过数理统计理论建立模型来确定。在实际预测中,可利用多元线性回归相关分析的计算机程序来实现。
是要估计的参数,可通过数理统计理论建立模型来确定。在实际预测中,可利用多元线性回归相关分析的计算机程序来实现。
5.对模型参数的估计值进行检验。
此项工作的目的在于判定估计值是否满意、可靠。一般检验工作须从以下几方面来进行。
- 经济意义检验
关于经济预测的数学模型,首先要检验模型是否有经济意义,γp若参数估计值的符号和大小与公路运输经济发展以及经济判别不符合时,这时所估计的模型就不能或很难解释公路运输经济的一般发展规律,就应抛弃这个模型,需要重新构造模型或重新挑选影响因素。
- 统计检验
统计检验是数理统计理论的重要内容,用于检验模型估计值的可靠性。通常,在公路客、货运量预测中应采用的统计检验是:
- 拟合度检验
所谓拟合度是指所建立的模型与观察的实际情况轨迹是否吻合、接近,接近到什么程度。统计学是通过构造统计量R2来度量的,R2可由样本数据计算得出。若建立的模型愈接近于实际,则R^2愈接近于1。
- 回归方程的显著性检验
回归方程的显著性检验是通过方差分析构造统计量F来进行的,统计量F是通过样本数据计算得出的。当给定某一置信度后,可以通过查阅F表来确定回归模型从总体效果来看是否可以采纳。
- 参数估计值的标准差检验
估计值的标准差是衡量估计值与真实参数值的离差的一种量度。参数的标准差越大,估计值的可靠性也就越小;反之,如果标准差越小,那么估计值的可靠性也就越大。参数值标准差的检验,可以通过构造大统计量来进行量度。当给定某一置信度后,可以通过查表来确定模型中某个参数估计值的可靠性。
应当强调指出,统计检验相对于经济意义检验来说是第二位的。如果经济意义检验不合理,那么即使统计检验可以达到很高的置信度,也应当抛弃这种估计结果,因为用这样的结果来进行经济预测是没有意义的。
6.最优回归方程的确定
经过上述的经济意义和统计检验后,挑选出的线性回归方程往往是好几个、为了从中优选出用于进行实际预测的方程,我们可以采用定性和定量相结合的办法。
从数理统计的原理来讲,应挑选方程的剩余均方较小为好,但作为经济预删还必须尽量考虑到方程中的影响因素更切合实际和其未来值更易把握的原则来综合考虑。当然、有时也可以从中挑选出好几个较优的回归方程,通过预测后,分别作为不同的高、中、低方案以供决策人员选择。
7.模型的实际预测检验
在获得模型参数估计值后,又经过了上述一系列检验而选出的最优(或较优)回归方程,还必须对模型的预测能力加以检验。不难理解、最优回归方程对于样本期间来说是正确的,但是对用于实际预测是否合适呢?为此,还必须研究参数估计值的稳定性及相对于样本容量变化时的灵敏度,也必须研究确定估计出来的模型是否可以用于样本观察值以外的范国,其具休做法是:
(1)采用把增大样本容量以后模型估计的结果与原来的估计结果进行比较,并检验其差异的显著性。
(2)把估计出来的模型用于样本以外某一时间的实际预测,并将这个预测值与实际的观察值作一比较,然后检验其差异的显著性。
8.模型的应用
公路客、货运输量多元线性回归预测模型的研究目的主要有以下几个方面。
(1)进行结构分析,研究影响该地区的公路客、货运输量的主要因素和各影响因素影响程度的大小,进一步探讨该地区公路运输经济理论。
(2)预测该地区今后年份的公路客、货运输量的变化,以便为公路运输市场、公路运输政策及公路运辅建设项目投资作出正确决策提供理论依据。另外,还可以通过公路客、货运输量与公路交通量作相关分析来对公路的饱和度发展趋势进行预测。从而为公路的新建、扩建项目的投资提供决策分析。
(3)模拟各种经济政策下的经济效果,以便对有关政策进行评价。
四、经调查分析,影响某地区旅客运输量的因素为:
x1——国民收入
x2——工农业总产值
x3——社会总产值
x4——人口
x5——客车保有量
x6——城乡居民储蓄存款
经计算得下列相关系数表:
| x1 | x2 | x3 | x4 | x5 | x6 | |
| Y | 0.9439 | 0.9287 | 0.9043 | 0.9914 | 0.9670 | 0.7021 |
| Z | 0.9736 | 0.96l4 | 0.9326 | 0.8645 | 0.9321 | 0.6678 |
Y——客运盈
Z——旅客周转量
若令α = 0.85,则可以舍去x6这个影响因素,也就是认为“城乡居民储蓄存款”不能作为响旅客运输量的主要因素。
2.经调查分析、影响某地区旅客运输量的因素为:
x1——国民收入
x2——工农业总产值
x3——社会总产值
x4——人口
x5——客车保有量
x6——国民生产总值
x7——公路通车里程
经计算得客运量和旅客周转量的经验线性回归方程如下:
Y = α0 + α1x1 + α2x2 + α5x5 R2 = 0.9997
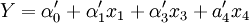 R2 = 0.9962
R2 = 0.9962
Z = β0 + β4x4 + β5x5 + β7x7 R2 = 0.9983
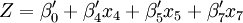 R2 = 0.9990
R2 = 0.9990
Y——客运盈
Z——旅客周转量
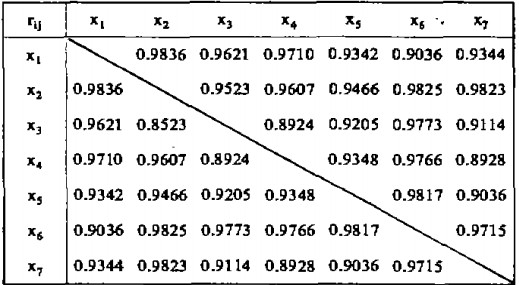
各自变量间的相关系数表如下:
由上述计算可知,四个方程中均未出现rij > R2的情况,因此可以认为各自方程中的影响因素之间不存在严重共线性问题。
3.经调查分析,影响某地区货运周转量的因素为:
x1——国民收入
x2——工农业总产值
x3——基建投资额
x4——原煤产量
x5——钢铁、化肥、水泥、粮食总产量
x6——国民总产值
x7——社会商品零售总额
x8——相邻地、市工农业总产值的平均值
Y = a0 + a4x4 + a6x6 + a7x7 (1)
其中:R2=0.9875 F=206.33 S·E=1673.24
t4=-2.8321 t6=3.1407 t7=2.7431
Y = b0 + b2x2 + b4x4 (2)
其中:R2=0.9764 F=164.59 S·E=1044.27
- ↑ 1.0 1.1 龚曙明.市场调查与预测/清华大学出版社, 2005 .ISBN 7810824708, 9787810824705
- ↑ 马进.公路客货运输量多元线性回归预测方法探讨[J].汽车运输研究.1994(1)
本条目由以下用户参与贡献
Angle Roh,funwmy,Zfj3000,Vulture,Xiangtaiyan,Cabbage,Fghghg,Yixi,Yongjieyan,Tears~,HEHE林,姜鹏,连晓雾,y桑,Tracy,寒曦,Jiang Ze,张雷,Mis铭,Llyn.评论(共39条)
太差了
条目内容若有不足或未完善,欢迎指正,或直接参与编辑。
关于“回归系数显著性检验”一段落中,回归系数的t检验值的计算公式没有列出,疑似只复制了文本而漏掉了图片?
谢谢指正,已进行修改完善
希望以后改善:输入“F检验”根本跳不到这个页面,搜索功能太差,很难找到自己想要的
由于F检验是重定向到方差分析里的,因此搜索的时候显示的会是方差分析
b1,b2如果出现负值表明什么含义
我也有同样的问题,如果是负值,能否照常使用?
您可进入多元非线性回归分析希望对您有帮助!
我有一个问题,一直也没搞清楚,想请教你一下。在多元回归线性回归分析之前,是否一定要做相关性分析?如果做相关性分析,那么它的作用或目的是什么?劳烦高手了?
我有一个问题,一直也没搞清楚,想请教你一下。在多元回归线性回归分析之前,是否一定要做相关性分析?如果做相关性分析,那么它的作用或目的是什么?劳烦高手了?
一定要做相关性分析,相关系数高的变量要剔除,为了保持各个变量之间的独立性,这样才能做多元的线性回归。
请教:如果是2组多元数据,因子相同,进行多元回归,得到2个多元回归方程,常数项基本相同,如2个方程:y=10x1+90x2+100,y=20x1+50x2+105,对于这2个方程可不可以认为相对于y,第2组样本x1因子的敏感性高于第1组样本,x2因子的敏感性低于第1组样本。谢谢!
自变量之彰是什么意思,看不明白
自变量之间,错别字,改了
解析失败 (PNG 转换失败; 请检查是否正确安装了 latex, dvips, gs 和 convert): x_1
写的太好了,就是很多图片没有
应改为间 // 因
谢谢指正,已修改








真棒