久期
出自 MBA智库百科(https://wiki.mbalib.com/)
久期(Duration)
目录[隐藏] |
什么是久期(Duration) [1]
久期有许多不同的形式和解释。几种尤为重要的种类是麦考莱久期(Macaulay duration)、修正久期(Modified duration)、封闭式久期(Closed-form duration)和有效久期(Effective duration)。
麦考莱久期(Macaulay duration)
久期的概念最早是马考勒(Macaulay)在1938年提出来的,所以又称马考勒久期(简记为D)。马考勒久期是使用加权平均数的形式计算债券的平均到期时间。它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。
“久期”又叫“持续期”,要归功于F.R•麦考莱,他在1938年提出要通过衡量债券的平均到期期限来研究债券的时间结构。当被运用于不可赎回债券时,麦考莱久期就是以年数表示的可用于弥补证券初始成本的货币加权平均时间价值。久期对于财务经理的主要价值在于它是衡量利率风险的直接方法,久期越长,利率风险越大。麦考莱久期有如下假设:收益率曲线是平坦的;用于所有未来现金流的贴现率是固定的。
保罗·萨缪尔森、约翰·斯克斯和瑞丁敦在随后的若干年独立地发现了久期这一理论范畴,特别是保罗·萨缪尔森和瑞丁敦将久期用于衡量资产/负债的利率敏感性的研究,使得久期具有了第二种含义,即:资产针对利率变化的价格变化率。
久期--的第二个含义是债券投资管理中的一个极其重要的策略----“免疫策略”的理论基础,根据该策略,当交易主体债券组合的久期与债权的持有期相等的时候,该交易主体短期内就实现了“免疫”的目标,即短期内的总财富不受利率波动的影响。
但是运用这一策略的前提则是,现有久期概念能否正确地衡量未来任何利率变动情景下债券价格的变动情况。
修正久期(Modified duration)
债券的修正久期帮助投资者理解,如果到期收益率(YTM)上升或下降1%,债券价格会上升或下降多少。
如果投资者担心短期内利率会发生变化,这是一个重要的指标。具有半年付息的债券的修正久期可以用以下公式计算:
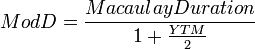
封闭式久期(Closed-form duration)
有效久期(Effective duration)
票面利率、到期时间、初始收益率是影响债券价格的利率敏感性的三个重要因素,它们与久期之间的关系也表现出一些规则。
- 1.保持其它因素不变,票面利率越低,息票债券的久期越长。
票面利率越高时,早期的现金流现值越大,占债券价格的权重越高,使时间的加权平均值越低,即久期越短。
- 2.保持其它因素不变,到期收益率越低,息票债券的久期越长。
到期收益率越低时,后期的现金流现值越大,在债券价格中所占的比重也越高,时间的加权平均值越高,久期越长。
- 3.一般来说,在其它因素不变的情况下,到期时间越长,久期越长。
债券的到期时间越长,价格的利率敏感性越强,这与债券的到期时间越长久期越长是一致的。但是,久期并不一定总随着到期时间的增长而增长。
![MacD=\frac{\sum_{t=1}^T PV(c_t)\times t}{P}=\sum_{t=1}^T[\frac{PV(c_t)}{P}\times t]](/w/images/math/1/5/e/15e569d6a15bea19c72448931376c522.png) (公式1)
(公式1)
其中,
- MacD是马考勒久期,
- P是债券当前的市场价格,
- PV(Ct)是债券未来第t期可现金流(利息或资本)的现值,
- T是债券的到期时间。
- t为从当前到t时刻现金流发生的持续时间。
- y为债券的风险程度相适应的收益率。假设未来所有现金流的贴现率都固定为y。
需要指出的是在债券发行时以及发行后,都可以计算马考勒久期。计算发行时的马考勒久期,T(到期时间)等于债券的期限;计算发行后的马考勒久期,T(到期时间)小于债券的期限。
![MacD=\frac{1+r}{r}-\frac{1+r+N\times (c-r)}{c\times [(1+r)^N-1]+r}](/w/images/math/d/2/0/d2015efbad53a4e5e8cedbb2dab489e0.png)
- D为久期;
- c为票息率
- r为市场利率
- N为到期期限;
任一金融工具的久期公式一般可以表示为[2]:
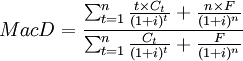 (公式2)
(公式2)
其中:
实际上,公式(公式3)的分母正是该金融工具的市场价值,因此,久期公式又可表示为:
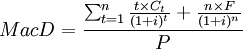 (公式3)
(公式3)
其中:P表示该金融工具的市场价值或价格。
久期的计算过程举例[2]
下面试举一例来说明久期的计算过程。假设面额为1000元的3年期变通债券,每年支付一次息票,年息票率为10%,此时市场利率为12%,则该种债券的久期为:
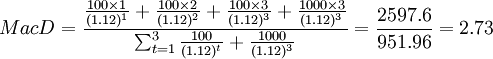 (年)
(年)
如果其他条件不变,市场利率下跌至5%,此时该种债券的久期为:
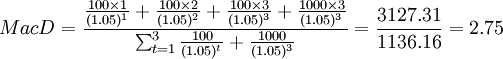 (年)
(年)
同理,如果其他条件不变,市场利率上升至20%,此时久期为:
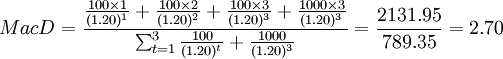 (年)
(年)
再者,如果其他条件不变,债券息票率为0,那么:
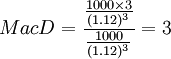 (年)
(年)
- 从上面的计算结果可以发现,久期随着市场利率的下降而上升,随着市场利率的升而下降,这说明两者存在反比关系。此外,在持有期间不支付利息的金融工具,其久期等于到期期限或偿还期限。那些分期付息的金融工具,其久期总是短于偿还期限,是由于同等数量的现金流量,早兑付的比晚兑付的现值要高。金融工具到期期限越长其久期也越长;金融工具产生的现金流量越高,其久期越短。
- 1.只有贴现债券的马考勒久期等于它们的到期时间
- 2.直接债券的马考勒久期小于或等于它们的到期时间
马考勒久期与债券价格的关系
对于给定的收益率变动幅度,马考勒久期越大,债券价格的波动幅度越大:
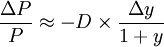
到期时间、息票率、到期收益率是决定债券价格的关键因素,与久期存在以下的关系:
- 1.零息票债券的久期等于到它的到期时间。
- 2.到期日不变,债券的久期随息票据利率的降低而延长。
- 3.息票据利率不变,债券的久期随到期时间的增加而增加。
- 4.其他因素不变,债券的到期收益率较低时,息票债券的久期较长。
债券的凸性准确地描述了债券价格与收益率之间非线性的反向关系;而久期将债券价格与收益率之间的反向关系视为线性的(一阶导数关系),只是一个近似公式。
凸性(C),实际上描述了债券价格和收益率的二阶导数关系。定义如下:
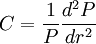
凸性(C)和马考勒久期(D)一起,可以更加准确地反映利率变动对债券价格的影响:
(泰勒级数二级展开)
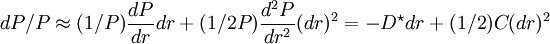
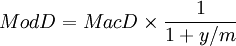
通常,久期值还得再除以1+y/m加以修正,y即债务工具的收益率,m为每年发生现金流的次数,这个修正久期用ModD表示,即ModD =MacD/(1+y/m)。
在债券分析中,久期已经超越了时间的概念,投资者更多地把它用来衡量债券价格变动对利率变化的敏感度,并且经过一定的修正,以使其能精确地量化利率变动给债券价格造成的影响。修正久期越大,债券价格对收益率的变动就越敏感,收益率上升所引起的债券价格下降幅度就越大,而收益率下降所引起的债券价格上升幅度也越大。可见,同等要素条件下,修正久期小的债券比修正久期大的债券抗利率上升风险能力强,但抗利率下降风险能力较弱。
正是久期的上述特征给我们的债券投资提供了参照。当我们判断当前的利率水平存在上升可能,就可以集中投资于短期品种、缩短债券久期;而当我们判断当前的利率水平有可能下降,则拉长债券久期、加大长期债券的投资,这就可以帮助我们在债市的上涨中获得更高的溢价。
需要说明的是,久期的概念不仅广泛应用在个券上,而且广泛应用在债券的投资组合中。一个长久期的债券和一个短久期的债券可以组合一个中等久期的债券投资组合,而增加某一类债券的投资比例又可以使该组合的久期向该类债券的久期倾斜。所以,当投资者在进行大资金运作时,准确判断好未来的利率走势后,然后就是确定债券投资组合的久期,在该久期确定的情况下,灵活调整各类债券的权重,基本上就能达到预期的效果。
久期是一种测度债券发生现金流的加权平均期限的方法。由于债券价格敏感性会随着到期时间的增长而增加,久期也可用来测度债券对利率变化的敏感性,根据债券的每次息票利息或本金的支付时间的加权平均来计算久期。
久期的计算就当是在算加权平均数。其中变量是时间,权数是每一期的现金流量,价格就相当于是权数的总和(因为价格是用现金流贴现算出来的)。这样一来,久期的计算公式就是一个加权平均数的公式了,因此,它可以被看成是收回成本的平均时间。
决定久期即影响债券价格对市场利率变化的敏感性包括三要素:到期时间、息票利率和到期收益率。
不同债券价格对市场利率变动的敏感性不一样。债券久期是衡量这种敏感性最重要和最主要的标准。久期等于利率变动一个单位所引起的价格变动。如市场利率变动1%,债券的价格变动3,则久期是3。
实际上,久期在数值上和债券的剩余期限近似,但又有别于债券的剩余期限。在债券投资里,久期被用来衡量债券或者债券组合的利率风险,它对投资者有效把握投资节奏有很大的帮助。
一般来说,久期和债券的到期收益率成反比,和债券的剩余年限及票面利率成正比。但对于一个普通的附息债券,如果债券的票面利率和其当前的收益率相当的话,该债券的久期就等于其剩余年限。还有一个特殊的情况是,当一个债券是贴现发行的无票面利率债券,那么该债券的剩余年限就是其久期。这也是为什么人们常常把久期和债券的剩余年限相提并论的原因。
另一种说法:久期是债券平均有效期的一个测度,它被定义为到每一债券距离到期的时间的加权平均值,其权重与支付的现值成比例 。
久期是考虑了债券现金流现值的因素后测算的债券实际到期日。价格与收益率之间是一个非线性关系。但是在价格变动不大时,这个非线性关系可以近似地看成一个线性关系。也就是说,价格与收益率的变化幅度是成反比的。值得注意的是,对于不同的债券,在不同的日期,这个反比的比率是不相同的。
久期的案例分析[3]
某附息债券的面值为1000元,剩余期限为3年,票面年利率为8%,每年付息一次。该债券市场价格为950.25元,因此该债券的到期收益率为10.00%。请计算该债券的久期是多少?
解:该附息债券剩余期限内会收回3笔现金流,分别是第一年的利息80元,第二年的利息80元,第三年的本金和利息之和1080元。现金流收回时间和现金流金额分别是表1中的第一列和第二列。三笔现金流发生的时间不一样,因此对应的现值(贴现)因子也不一样。按照三个贴现因子,三笔现金流贴现到现在的现值分别是72.73元、66.12元和811.40元。贴现计算如下:
第一笔现金流贴现值=第一笔现金流金额×第一笔现金流贴现因子
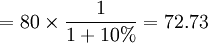 (元)
(元)第二笔现金流贴现值=第二笔现金流金额×第二笔现金流贴现因子
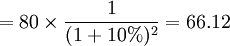 (元)
(元)第三笔现金流贴现值=第三笔现金流金额×第三笔现金流贴现因子
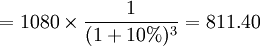 (元)
(元) 其中,第一笔现金流贴现因子为 ,第二笔现金流贴现因子为
,第二笔现金流贴现因子为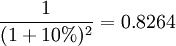 ,第三笔现金流贴现因子为
,第三笔现金流贴现因子为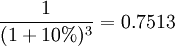 。贴现因子和现金流现值分别是表5.2中的第三列和第四列。
。贴现因子和现金流现值分别是表5.2中的第三列和第四列。
现金流之和950.25即为债券价格P0,表1的第五列是各期现金流现值PV(Ct)和现金流收回时间t的乘积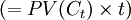 ,以及乘积之和2639.17元
,以及乘积之和2639.17元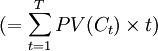 。用乘积之和除以P0就得到债券的久期为2.78年。
。用乘积之和除以P0就得到债券的久期为2.78年。
久期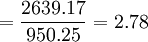 (年)
(年)
表1 久期计算细表
| 现金流收回时间 | 现金流金额 | 现值(贴现)因子 | 现金流现值 | 现金流现值×现金流收回时间 |
| 1 | 80 | 0.9091 | 72.73 | 72.73 |
| 2 | 80 | 0.8264 | 66.12 | 132.23 |
| 3 | 1080 | 0.7513 | 811.40 | 2434.21 |
| 950.25 | 2639.17 |
- ↑ Bond duration-Wikipedia
- ↑ 2.0 2.1 郑鸣.商业银行管理学[M].清华大学出版社, 2005.ISBN:7302101256, 9787302101253
- ↑ 岑仲迪 顾锋娟编著.证券投资学.清华大学出版社,2011.02.
本条目由以下用户参与贡献
Lolo,Zfj3000,Angle Roh,Dan,Ania,Dionwang,Vulture,Dawinetion,Franklee0415,Guyu1016,风行水使,Scuibk,Cqzxmw,Yixi,连晓雾,林巧玲,可恨密码记不住,方小莉,李文诚,苏青荇,〢.蔠嚸,LuyinT,M id 731f627d96217404746689a7b388d1a5,AleAle.评论(共33条)
有点简单了,不知是否可以补充得更详细一些?
已对内容进行了补充,期待网友参与完善
谢谢您的贡献,MBA智库百科的发展离不开大家的参与及完善
“需要说明的是,久期的概念不仅广泛应用在个券上,而且广泛应用在债券的投资组合中。一个长久期的债券和一个短久期的债券可以组合一个中等久期的债券投资组合,而增加某一类债券的投资比例又可以使该组合的久期向该类债券的久期倾斜。所以,当投资者在进行大资金运作时,准确判断好未来的利率走势后,然后就是确定债券投资组合的久期,在该久期确定的情况下,灵活调整各类债券的权重,基本上就能达到预期的效果。”
这里可以再具体说明下么?
公式要这么复杂么?
还好啦 只用到求和、一阶导数,没有用更复杂的高等数学~
久期这一概念已经被广泛用来检测交易组合对于利率曲线的风险暴露。顾名思义,金融产品的久期是指投资人收到一比投资的所有现金流支付平均需要等待的时间。一个N年期零利息国债的久期为N年,而一个N年带息(coupon-bearing)国债的久期小于N年,这是因为国债持有人在N年之前就已经收到某些现金流支付。---详细见《风险管理与金融机构》(《risk management and financial institutions》)作者:约翰。赫尔(John C.Hull)多伦多大学
到期日不变,债券的久期随息票据利率的降低而延长。 一般来说,久期和债券的到期收益率成反比,和债券的剩余年限及票面利率成正比。这篇文章自相矛盾啊,久期和票面利率成反比!!!请改正。
到期日不变,债券的久期随息票据利率的降低而延长。 一般来说,久期和债券的到期收益率成反比,和债券的剩余年限及票面利率成正比。这篇文章自相矛盾啊,久期和票面利率成反比!!!请改正。
也有相同疑问。 请学习精湛者赐教。
可否对“免疫策略”加以分析?
可参考条目免疫策略,希望对您有帮助!~
智库真是太牛啦,我英语教科书上面难以理解的知识点这里都有解释,我一本教科书1000人民币这里的知识全部不用收费哈哈,光凭这点还是我们中国好啊~~
是很专业啊,大学数学以前太荒废了。
"一般来说,久期和债券的到期收益率成反比,和债券的剩余年限及票面利率成正比。但对于一个普通的附息债券,如果债券的票面利率和其当前的收益率相当的话,该债券的久期就等于其剩余年限。 " 这一段有问题有问题。票面利率等于当前收益率久期也小于剩余年限;票面利率与久期的关系也不对。

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 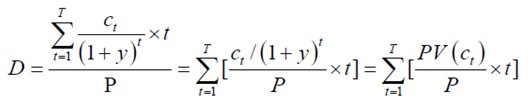










有点简单了,不知是否可以补充得更详细一些?