DURATION函数
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
什么是DURATION函数[1]
DURATION(Returns the Macauley duration for an assumed par value of $100. Duration is defined as the weighted average of the present value of the cash flows and is used as a measure of a bond price's response to changes in yield.)
为假定票面值为$100的债券返回麦考利持续时间。持续时间定义为一系列现金流现值的加权平均值,用于计量债券价格对于收益率变化的敏感程度。
DURATION函数用于返回假设面值¥100的定期付息有价证券的修正期限(麦考利久期)。期限定义为一系列现金流现值的加权平均值,用于计量债券价格对于收益率变化的敏感程度。
DURATION函数的语法和参数[1]
语法
- DURATION(settlement,maturity,coupon,yld,frequency,basis)
要点
应使用DATE函数输入日期,或者将函数作为其他公式或函数的结果输入。例如,使用函数 DATE(2008,5,23) 输入2008年5月23日。如果日期以文本形式输入,则会出现问题。
- Settlement 为证券的结算日。结算日是在发行日之后,证券卖给购买者的日期。
- Maturity 为有价证券的到期日。到期日是有价证券有效期截止时的日期。
- Coupon 为有价证券的年息票利率。
- Yld 为有价证券的年收益率。
- Frequency 为年付息次数,如果按年支付,frequency = 1;按半年期支付,frequency = 2;按季支付,frequency = 4。
- Basis 为日计数基准类型。
| BASIS | 日计数基准 |
|---|---|
| 0 或省略 | US (NASD) 30/360 |
| 1 | 实际天数/实际天数 |
| 2 | 实际天数/360 |
| 3 | 实际天数/365 |
| 4 | 欧洲 30/360 |
注解
- Microsoft Excel 可将日期存储为可用于计算的序列数。默认情况下,1900年1月1日的序列号是1,而2008年1月1日的序列号是39448,这是因为它距1900年1月1日有39448天。
- Microsoft Excel for the Macintosh 使用另外一个默认日期系统。
- 结算日是购买者买入息票(如债券)的日期。到期日是息票有效期截止时的日期。例如,在2008年1月1日发行的30年期债券,六个月后被购买者买走。则发行日为 2008年1月1日,结算日为2008年7月1日,而到期日是在发行日2008年1月1日的30年后,即2038年1月1日。
- Settlement、maturity、frequency 和 basis 将被截尾取整。
- 如果 settlement 或 maturity 不是合法日期,函数 DURATION 返回错误值 #VALUE!。
- 如果 coupon<0 或 yld<0,函数 DURATION 返回错误值 #NUM!。
- 如果 frequency 不是数字 1、2 或 4,函数 DURATION 返回错误值 #NUM!。
- 如果 basis<0 或 basis>4,函数 DURATION 返回错误值 #NUM!。
- 如果 settlement≥maturity,函数 DURATION 返回错误值 #NUM!。
任一金融工具的久期公式一般可以表示为[2]:
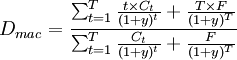 (公式2)
(公式2)
其中:
息票债券的久期
- c表示每期票面利率
- y表示每期到期收益率
- T表示距到期日的期数
麦考利久期一般(公式2)可简化为,
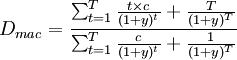
根据年金计算方法,再加以数学推导得:
- ★
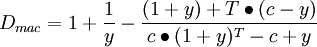
当息票债券平价出售时,到期收益率与票面利率相等,可进一步简化公式。麦考利久期一般公式可简化为
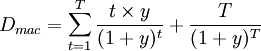
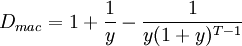
- 注意,从上式中求出的久期是以期数为单位的,我们还要把它除以每年付息的次数,转化成以年为单位的久期。
例:面值为100 元,票面利率为8%的三年期债券,半年付息一次,下一次付息在半年后。如果到期收益率为10%,计算它的麦考利久期。
解:该债券的麦考利久期是5.4351个半年,也就是5.4351/2=2.7176年
案例一:[3]
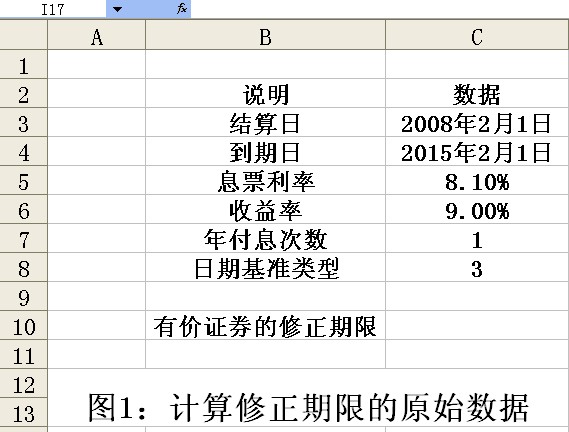
例如,假设某人购买有价证券的结算日是2008年2月1日,到期日是2015年2月1日,息票利率为8.1%,收益率为9%,如果按照实际天数/365为日计数基准,以一年期支付,现利用DURATION函数计算有价证券的修正期限。具体的操作步骤如下:
1.在Excel 2010主窗口打开的工作表中输入基础数据,如图1所示。
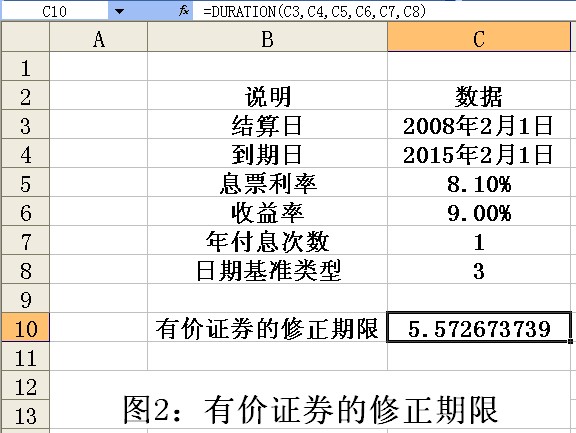
2.选中C1O单元格,在其中输入公式“=DURATION(C3,C4,C5,C6,C7,C8)”,按(Enter)键,即可得到有价证券的修正期限,如图2所示。
- ↑ 1.0 1.1 DURATION函数.微软中国官网
- ↑ 郑鸣.商业银行管理学[M].清华大学出版社, 2005.ISBN:7302101256, 9787302101253
- ↑ 武新华,段铃华等著.第八章 财务与财务分析函数 Excel2010函数与公式速查宝典.北京:机械工业出版社,2011.03.







