莖葉圖
出自 MBA智库百科(https://wiki.mbalib.com/)
莖葉圖(Stem and leaf plot)
目錄 |
莖葉圖又稱“枝葉圖”,它的思路是將數組中的數按位數進行比較,將數的大小基本不變或變化不大的位作為一個主幹(莖),將變化大的位的數作為分枝(葉),列在主幹的後面,這樣就可以清楚地看到每個主幹後面的幾個數,每個數具體是多少。
莖葉圖有三列數:左邊的一列數統計數,它是上(或下)向中心累積的值,中心的數(帶括弧)表示最多數組的個數;中間的一列表示莖,也就是變化不大的位數;右邊的是數組中的變化位,它是按照一定的間隔將數組中的每個變化的數一一列出來,象一條枝上抽出的葉子一樣,所以人們形象地叫它莖葉圖。
莖葉圖是一個與直方圖相類似的特殊工具,但又與直方圖不同,莖葉圖保留原始資料的資訊,直方圖則失去原始資料的訊息。將莖葉圖莖和葉逆時針方向旋轉9O度,實際上就是一個直方圖,可以從中統計出次數,計算出各數據段的頻率或百分比。從而可以看出分佈是否與正態分佈或單峰偏態分佈逼近。
莖葉圖在質量管理上用途與直方圖差不多,但它通常是作為更細緻的分析階段使用。由於它是用數字組成直方圖,所以在做的時候比直方圖時,通常我們常使用專業的軟體進行繪製。
1、用莖葉圖表示數據有兩個優點:一是從統計圖上沒有原始數據信息的損失,所有數據信息都可以從莖葉圖中得到;二是莖葉圖中的數據可以隨時記錄,隨時添加,方便記錄與表示。
2、莖葉圖只便於表示兩位有效數字的數據,而且莖葉圖只方便記錄兩組的數據,兩個以上的數據雖然能夠記錄,但是沒有表示兩個記錄那麼直觀、清晰。
莖葉圖的案例分析[1]
莖葉圖是將統計分組和次數分配一次完成,是探索性數據分析中對數據的初步形象描繪。其圖形直觀且保留原始信息,均值、中位數和眾數均可依原始數據準確方便地算出。現以某班一次考試成績為例,介紹莖葉圖的作法。
作圖過程是先作“莖”後填“葉”,將分組標誌(組距)視為莖,按數的大小從上到下(也可從下到上)排列。將每一個觀察值視為一個樹葉,每一個樹葉按照樹莖之要求長在應長的樹莖上。對於百分制的考試分數,先將高位數字按順序排成一列,後將每個分數的個位數為葉長在相應的莖上,最後將每莖上的葉按從大到小的排列。若人數較多,樹葉較長,可將高位數重覆兩次,個位數分為0~5一枝,5~9一枝。圖1即為最後完成的莖葉圖表。為了便於分析,可將1/4、3/4分位數及中位數用符號標出。
利用莖葉圖對考試成績進行評估
1、班級內成績評估
1)將莖葉圖莖和葉逆時針方向旋轉9O度,實際上就是一個班級成績帶有數字的直方圖,可以從中統計出次數,計算出各分數段的頻率或百分比,從它可以看出班級成績的分佈是否與正態分佈或單峰偏態分佈逼近。
2)若莖葉圖成績表扁而寬(如圖1),說明該班整體成績較集中,成績差異不大;如果莖葉圖長而窄,說明該班成績較分散,標準差較大,高分低分差距大。這可使教師或校管理部門對學生成績有所瞭解。
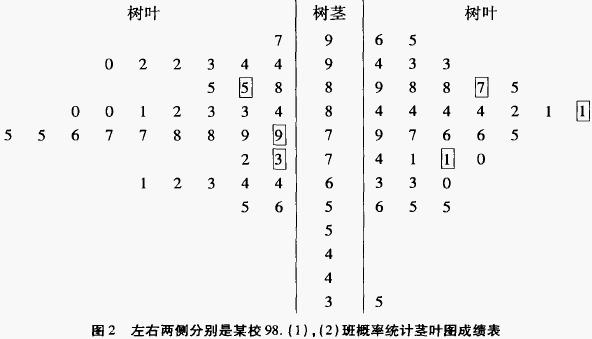
3)異常成績的發現及處置。莖葉圖成績表中若有少數成績遠離中位數,如圖2中右側,說明這類學生與一般學生有質的區別,對於優秀的學生應加以培養,對於差的學生應找出根源加以幫助。這些異常值在計算標準差時可剔除,如圖2右側,x=77.1,標準差σ = 12.6,剔除異常值後,x=78.3,σ = 10.8,這樣可更科學地反映平均成績。
4)科學反映學生在班級中的名次。莖葉圖成績表中的成績被帶有方框的字分成4個區域,依次代表四個不同的水平,各層次學生都占總數的25% 。例如,圖2對應的某一學生考了75分,在右側的二班是中等水平,而在左側的一班只屬下等水平,這樣比較避免了以絕對分數來判定學生的成績。
2、班級間學生的評估
要對平行班同一課程的成績比較,可將兩個班的成績作為葉長在同一莖上,分別自左右兩側擴張,如圖2對照起來,簡明多了。若要對多個班級成績進行比較,可將莖葉垂直方向平行移動,作為莖葉圖。先將莖葉圖看成直方圖觀察兩班成績整體分佈狀況。若兩班成績圖形均接近正態分佈且中位數接近,說明兩班的成績差別不大;若兩側的峰值相距較遠,中位數差別大,說明兩班總體成績相差較大。
1)若對同一教師任教的平行班莖葉圖表進行比較,先看1/4,3/4分位數和中位數,如果兩個班的中位數較接近,說明其成績沒有顯著性差異,如果中位數接近,而莖葉圖的形狀有較大差異,從總體上來看成績差異不大,但圖形長而窄的班級兩極分化較大,教學難度大。如果中位數差別較大,則說明兩個班級學生的基礎,學習風氣有較大差異。對不同教師平行班比較時,中位數高的班級整體水平較高。
2)計算出左右兩側的H一散佈,即1/4位數與3/4位數的差。圖(2)中左H一散佈為10分,右H一散佈為16分,由此看到左側中等水平的學生成績差距並不大,競爭激烈,而右圖中的中等水平之間差距較大,教學有一定的難度。
3、結論
莖葉圖法是數理統計中數據分析的一種方法,將它應用到成績評估中,可保留原始分數,對學生成績作出科學化評價。其特點是做法簡單,評價全面,為教師和教學管理部門提供了一種教學質量評估的方法。
- ↑ 袁璐.數理統計的莖葉圖法及其應用.青島遠洋船員學院學報.2002年4期
評論(共29條)
莖葉圖一般只適於表示兩位有效數字的數據,如果大於或小於兩位,可以設定莖寬,如123,則莖寬設為10,在莖葉圖上表示為 1 | 2 ;如0.123,則莖寬設為0.1,莖葉圖表示為 1 | 2 。其實也可以自設葉寬,但一般很少這麼做,雖然更利於提高讀取原始數據的精度,但對圖形的長寬比例影響很大,影響形象分析。
莖葉圖一般只適於表示兩位有效數字的數據,如果大於或小於兩位,可以設定莖寬,如123,則莖寬設為10,在莖葉圖上表示為 1 | 2 ;如0.123,則莖寬設為0.1,莖葉圖表示為 1 | 2 。其實也可以自設葉寬,但一般很少這麼做,雖然更利於提高讀取原始數據的精度,但對圖形的長寬比例影響很大,影響形象分析。
如0.123,則莖寬設為0.01 -_-!!!
如0.123,則莖寬設為0.01 -_-!!!
那葉怎麼辦?
如0.123,則莖寬設為0.01 -_-!!!
我覺得[如0.123,則莖寬設為0.1,莖葉圖表示為 1 | 2 。]是對的,[如123,則莖寬設為10,在莖葉圖上表示為 1 | 2 ]這個好像不對哦
哦,,我曉得了,,,,是這樣的,,,123,莖寬是10,莖葉圖上是12 | 3,,近似值=(莖+葉)*莖寬=(12+0.3)*10=123... 如果是0.123,莖葉圖上是12 | 3,但莖寬是0.01... 近似值=(莖+葉)*莖寬=(12+0.3)*0.01=0.123









說的太好了!