回歸分析預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
回歸分析預測法(Regression Analysis Prediction Method)
目錄 |
回歸分析預測法,是在分析市場現象自變數和因變數之間相關關係的基礎上,建立變數之間的回歸方程,並將回歸方程作為預測模型,根據自變數在預測期的數量變化來預測因變數關係大多表現為相關關係,因此,回歸分析預測法是一種重要的市場預測方法,當我們在對市場現象未來發展狀況和水平進行預測時,如果能將影響市場預測對象的主要因素找到,並且能夠取得其數量資料,就可以採用回歸分析預測法進行預測。它是一種具體的、行之有效的、實用價值很高的常用市場預測方法。
回歸分析預測法有多種類型。依據相關關係中自變數的個數不同分類,可分為一元回歸分析預測法和多元回歸分析預測法。在一元回歸分析預測法中,自變數只有一個,而在多元回歸分析預測法中,自變數有兩個以上。依據自變數和因變數之間的相關關係不同,可分為線性回歸預測和非線性回歸預測。
1.根據預測目標,確定自變數和因變數
明確預測的具體目標,也就確定了因變數。如預測具體目標是下一年度的銷售量,那麼銷售量Y就是因變數。通過市場調查和查閱資料,尋找與預測目標的相關影響因素,即自變數,並從中選出主要的影響因素。
2.建立回歸預測模型
依據自變數和因變數的歷史統計資料進行計算,在此基礎上建立回歸分析方程,即回歸分析預測模型。
3.進行相關分析
回歸分析是對具有因果關係的影響因素(自變數)和預測對象(因變數)所進行的數理統計分析處理。只有當變數與因變數確實存在某種關係時,建立的回歸方程才有意義。因此,作為自變數的因素與作為因變數的預測對象是否有關,相關程度如何,以及判斷這種相關程度的把握性多大,就成為進行回歸分析必須要解決的問題。進行相關分析,一般要求出相關關係,以相關係數的大小來判斷自變數和因變數的相關的程度。
4.檢驗回歸預測模型,計算預測誤差
回歸預測模型是否可用於實際預測,取決於對回歸預測模型的檢驗和對預測誤差的計算。回歸方程只有通過各種檢驗,且預測誤差較小,才能將回歸方程作為預測模型進行預測。
5.計算並確定預測值
利用回歸預測模型計算預測值,並對預測值進行綜合分析,確定最後的預測值。
應用回歸預測法時應首先確定變數之間是否存在相關關係。如果變數之間不存在相關關係,對這些變數應用回歸預測法就會得出錯誤的結果。
正確應用回歸分析預測時應註意:
①用定性分析判斷現象之間的依存關係;
②避免回歸預測的任意外推;
③應用合適的數據資料;
案例一:回歸分析預測法預測新田公司銷售[1]
一、新田公司的發展現狀
新田公司全稱為新田摩托車製造有限公司,成立於1992年3月,當時的錫山市(那時還叫無錫縣)有兩個生產摩托車的鄉鎮企業:查橋鎮的捷達摩托車廠和洛社鎮的雅西摩托車廠。在9l、92年這兩家廠可以說是如日中天,但這兩家廠又各具特點:雅西摩托車廠完全是自主生產,除發動機外其餘配件都由本廠生產;捷達摩托車廠則是裝配型廠,配件由其他廠家生產,本廠只是組裝(後來也發展成了連發動機都生產的綜合型企業)。顧建新當時還只是一家村辦企業的供銷員,他就瞄準了摩托車行業的發展前景,於是想方設法和捷達廠取得了聯繫,從1992年3月起為捷達廠生產兩種型號的減震器,廠名是無錫減震器廠,由此開始了企業發展的道路。
減震器廠自成立以後,隨著捷達摩托車廠摩托車年產量的不斷增長而得到了迅速發展。到了1994年6月,顧建新終於有了一個極好的機會:捷達摩托車廠的銷售部門和捷達摩托車的銷售商產生了予盾,因此捷達摩托車的銷售商答應顧建新,若顧建新也能生產出和捷達差不多質量的摩托車,則他們會在相同條件下優先銷售顧建新生產的摩托車。有了這個承諾,顧建新於94年lO月就成立了新田摩托車製造有限公司,開始生產新田牌摩托車。
新田公司成立以後,在顧總和匡建中總工程師的領導下,開始了艱苦的創業過程,經過六年多的奮鬥,薪田公司終於從一個20多人的小廠發展成瞭如今的工人總數超過400人,日產摩托車超過200輛,年利潤超過2000萬的集團型企業,新田摩托車的配件包括發動機在內都由本企業自主生產。
新田公司如今已是一個企業集團,除公司本部(總裝廠)外,還有減震器廠、發動機廠、塑件廠、車架車間、油箱車間、噴塗車間等獨立部門,這些部門除滿足新田公司所需配件外,還可以對外供應。1999年底,由於摩托車市場競爭的日趨激烈,新田公司的銷售模式由代理制轉向了派員銷售制(由公司往各城市直接派出銷售人員,負責各城市的銷售工作),以減少中間環節,確保公司產品在整個摩托車市場的競爭力。同時,由於銷售模式的轉變,也帶來了生產模式的變化:以前是根據各地代理商的訂貨量來組織生產,現在則必需根據銷售情況和對將來銷售情況的預期來組織生產,這給企業的生產組織帶來了極大的困難。
2.新田公司銷售的歷史數據及要解決的問題
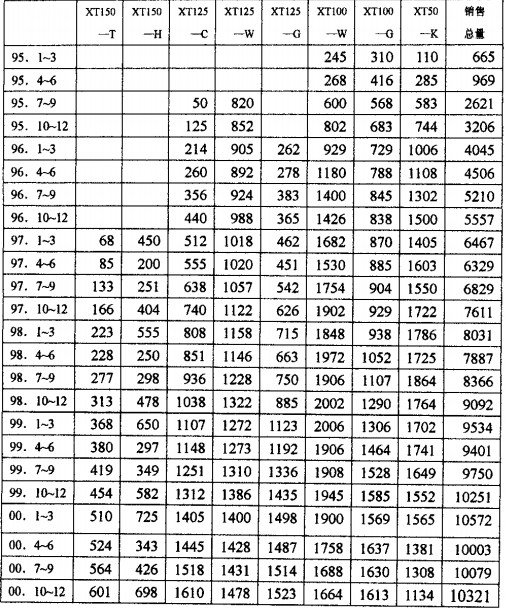
新田公司自94年成立以來取得了飛躍性的發展,這可以從新田公司歷年的銷售數據中看出來。下麵所附的表就是新田公司主導產品的銷售數據。(參見下麵表1.2.3.4)
從表中的數據可以看出,新田公司的生產銷售形勢還是比較好的,從總體上來說是處於上升趨勢,但某些車型的銷售也有下降趨勢。同時,還有一些問題從銷售數據上是看不出來的。自從公司實行派員銷售制以來,由於銷售的預期值估計不准,常常出現工人加班加點仍趕不上交貨對間的情況和工人上了班卻無事可做的情況。顧建新總經理和其他公司領導也都發現了這個問題,也找到了原因所在,但由於技術上的原因而無法解決。因此,新田公司目前急需解決的問題就是如何來進行準確可行的銷售預測,以保證公司的正常運行。
新田公司2001年第一季度銷售數據
| XT150-T | XT150-H | XT125-C | XT125-W | XT100-W | XT100-G | XT50-K | 總數 |
| 665 | 897 | 1660 | 1500 | 1529 | 1608 | 933 | 10372 |
新田公司2001年第二季度銷售數據
| XT150-T | XT150-H | XT125-C | XT125-W | XT100-W | XT100-G | XT50-K | 總數 |
| 668 | 350 | 1808 | 1581 | 1542 | 1503 | 1603 | 9862 |
新田公司XT50-M在無錫的銷售數據
| 第一季度 | 第二季度 | 第三季度 | 第四季度 | |
| 1996年 | 150 | 170 | 172 | 180 |
| 1997年 | 201 | 230 | 233 | 245 |
| 1998年 | 258 | 292 | 284 | 298 |
| 1999年 | 283 | 255 | 209 | 199 |
| 2000年 | 175 | 160 | 122 | 90 |
二、回歸分析預測法分析
回歸分析預測法是通過研究分析一個應變數對一個或多個自變數的依賴關係,從而通過自變數的已知或設定值來估計和預測應變數均值的一種預測方法。
回歸分析預測法又可分成線性回歸分析法、非線性回歸分析法、虛擬變數回歸預測法三種。這三種預測方法在新田公司銷售預測中都可以運用。
(一)線性回歸分析法的運用
線性回歸預測法是指一個或一個以上自變數和應變數之間具有線性關係(一個自變數時為一元線性回歸,一個以上自變數時為多元線性回歸),配合線性回歸模型,根據自變數的變動來預測應變數平均發展趨勢的方法。
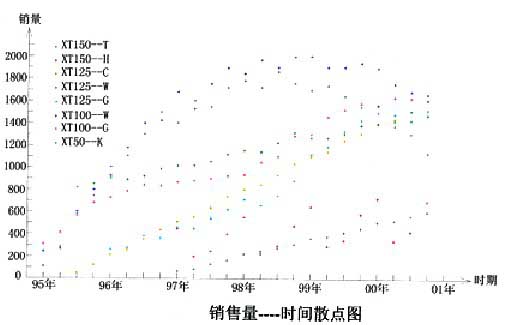
線性回歸預測法在銷售預測中用得比較多,根據新田公司銷售數據的散點圈分析,作者發現新田公司的XTl50~T、XTl25~C XTl25一W三種車型的銷售可以用一元線性回歸預測法進行預測,由於銷售數據是時間性序列,多元線性回歸在此不適用。
1.預測模型
由於新田公司銷售預測中只用到一元線性回歸預測法,而一元線性回歸又是一種廣泛應用並且比較簡單的預測方法,因此,只需對一元線性回歸模型作簡單介紹。
設X為自變數,Y為應變數,Y與X之間存在某種線性關係,一元線性回歸模型為:
yi = a + bxi + εi 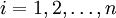 (1)
(1)
式中ε為各種隨機因素y的影響總和,ε − (0,σ2);y-N(a+bx,σ2)。則可設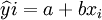 (2)
(2)
對此,可以通過最小二乘法來估計模型的回歸繫數。根據最小平方原理,必須符合以下條件:
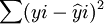 =最小值 (3)
=最小值 (3)
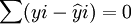 (4)
(4)
根據最小二乘法要求,記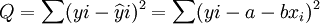
根據極值原理,為使Q具有最小值,可分別對a、b求偏導數,並令其等於零,即
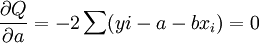
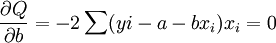
整理的:
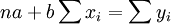
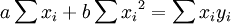
對上兩式聯立求解,即可得到回歸繫數的估計值:
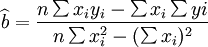 (5)
(5)
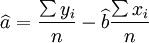 (6)
(6)
相關係數R可根據最小二乘原理及平均數的數學性質得到:
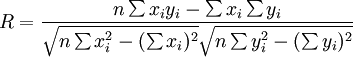 (7)
(7)
相關係數R的絕對值的大小表示相關程度的高低。
①當R=0時,說明是零相關,所求回歸繫數無效。
②當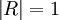 時,說明是完全相關,自變數X與應變數Y之間的關係為函數系。
時,說明是完全相關,自變數X與應變數Y之間的關係為函數系。
⑧當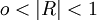 時,說明是部分相關,淵值越大相關程度越高。
時,說明是部分相關,淵值越大相關程度越高。
另外,估計標準差Sy,和預測區間公式參見《預測與決策技術》。
估計標準差: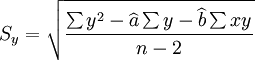 (8)
(8)
預測區間: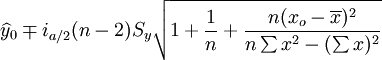 (9)
(9)
在上式中,a為顯著水平,n-2為自由度,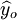 為y在xo的估計值。
為y在xo的估計值。
2.預測計算
根據上面介紹的預測模型,下麵就先計算XTl50-T在2001年第一季度的預測銷售量。
根據XTl50-T的銷售數據有:(X為時間,Y為銷售量)。
n=16;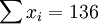 ;
;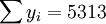 ;
;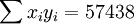 ;
;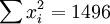 ;
;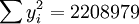
根據公式(5)、(6)、(7)、(8)、(9)有:
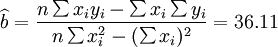
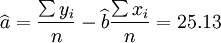
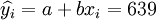 (xi = 17)
(xi = 17)
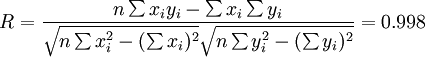
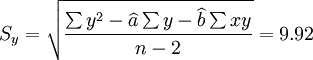
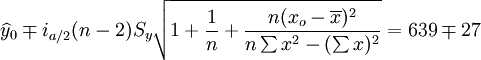
i0.025(14) = 2.145
以上是XT150-T的銷售預測計算,同理可計算XT125-C、XT150-W的預測結果,這裡不再給出計算過程而直接寫出結果:
①XTl25-C的預測結果:
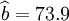 ;
;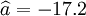 ;
;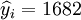 ;R=0.99 ;Sy = 16.56
;R=0.99 ;Sy = 16.56
預測區間為:(1641,1723) (i0.025(20) = 2.086)
②XTl25-W的預測結果:
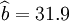 ;
;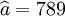 ;
;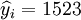 ;R=0.99 ;
;R=0.99 ;
Sy = 29.35
預測區間為:(1450,1596) (i0.025(20) = 2.086)
3.預測結果分析
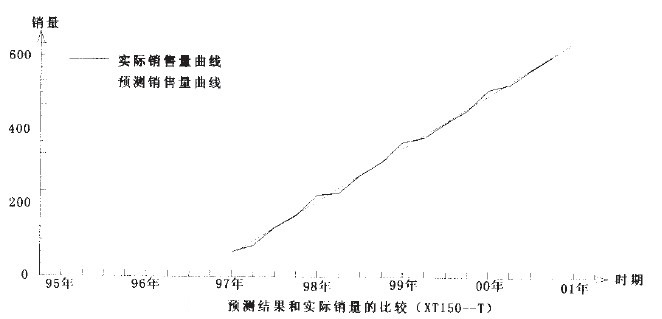
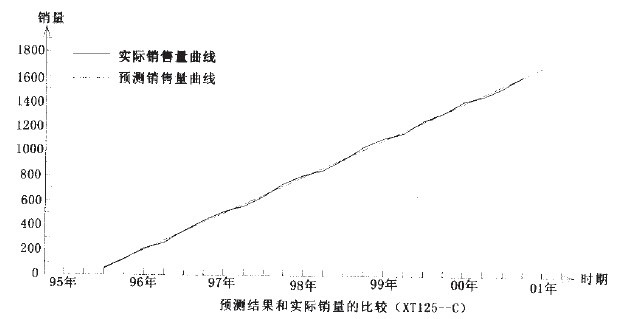
從上面的預測結果來看,有一點非常奇怪,那就是三種車型的預測中,相關係數R都非常接近於“1”,也就是說,這三種車型的銷售量和時間基本上是線性關係,相關程度非常之高。對於這個結果,作者感到很驚訝,為此,特意找到了新田公司,詢問這三種車型的銷售狀況,這才找到了原因。原來,這三種車型是新田公司的形象產品,基本上沒有利潤,和其他品牌的同類車型相比具有較大的的競爭力,因而這三種車型的銷售情況一直很好。公司為了其形象,對這三種車型採取計劃供應的方式,按逐年遞增的方式供應市場,以使這三種車型一直保持供不應求。由於以上原因,相關係數接近於“1”也就不奇怪了。
另外,作者把通過公式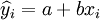 計算得到的各期銷售數和實際銷售量比較發現,這三種車型有一個共同特點,那就是:第一季度的預測值一般要比實際值大,而第二季度則相反。第三、四季度則預測值和實際值相近。仔細分析原因,可能是因為這三種車型價格都比較高,受年終分配影響,第一季度銷量自然較大,隨後的第二季度銷量就自然偏小。
計算得到的各期銷售數和實際銷售量比較發現,這三種車型有一個共同特點,那就是:第一季度的預測值一般要比實際值大,而第二季度則相反。第三、四季度則預測值和實際值相近。仔細分析原因,可能是因為這三種車型價格都比較高,受年終分配影響,第一季度銷量自然較大,隨後的第二季度銷量就自然偏小。
對比2001年第一季度的預測值和實際值,以及上面說到的兩個特點可以發現,XT150-T的預測結果比較正常,而XTl25-C、XTl25-W的預測值卻出現了反而比實際值大的反常情況。通過各期預測值和實際值比較發現,原來XTl25-W從99年第二季度開始就出現預測值大於實際值的情況,根據作者對摩托車市場的瞭解,認為可能是因為這種車型的銷路已經出現問題,不能保持供不應求了。
XTl25-C可能也是這種情況,只不過該車型的滯銷出現得稍稍晚而已。通過和新田公司銷售部門的聯繫發現,作者的判斷是正確的。
(二)非線性回歸預測法的運用
非線性回歸預測法是指自變數與因變數之間的關係不是線性的,而是某種非線性關係時的回歸預測法。非線性回歸預測法的回歸模型常見的有以下幾種:雙曲線模型、二次曲線模型、對數模型、三角函數模型、指數模型、冪函數模型、羅吉斯曲線模型、修正指數增長模型。
通過對新田公司銷售數據的散點圖分析發現,XT100-W和XT50-K這兩種車型的圖形接近於拋物線形狀,因此可用非線性回歸的二次曲線模型來預測。
1.預測模型
非線性回歸二次曲線模型為: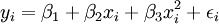 (10)
(10)
令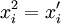 ,則模型變化為:
,則模型變化為: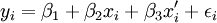 (11)
(11)
上式的矩陣形式為:Y = XB + ε (12)
用最小二乘法作參數估計,可設觀察值與模型估計值的殘差為E,則
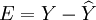 ,
,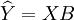
根據小二乘法要求有:
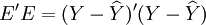 =最小值, (13)
=最小值, (13)
即: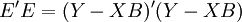 =最小值
=最小值
由極值原理,根據矩陣求導法,對B求導,並令其等於零,得:
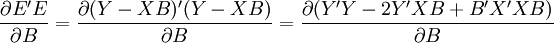
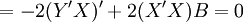
整理得回歸繫數向量B的估計值為: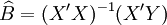 (14)
(14)
二次曲線回歸中最常用的檢驗是R檢驗和F檢驗,公式如下:
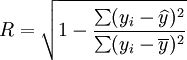 (15)
(15)
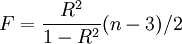 (16)
(16)
在實際工作中,R的計算可用以下簡捷公式:
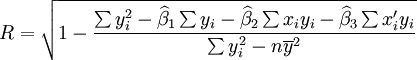 (17)
(17)
估計標準誤差為:
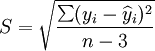 (18)
(18)
預測區間為:
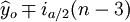 ·S (n<30) (19)
·S (n<30) (19)
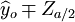 ·S (n>30) (20)
·S (n>30) (20)
2.預測計算
根據上面介紹的預測模型,下麵就先進行XT100-W的預測計算。
根據XTl00-W的銷售數據及(11)、(14)、(17)、(18)、(19)有(xi為時間變數):
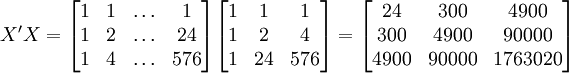
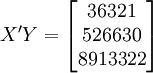 。
。
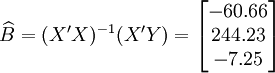
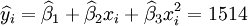 (x_i=25)
(x_i=25)
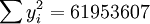 ;
;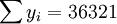 ;
;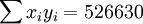 ;
;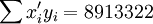
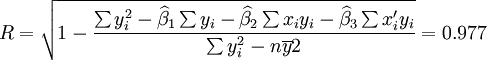
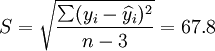
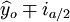 (n-3)·
(n-3)·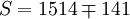 (i0.025(21) = 2.080)
(i0.025(21) = 2.080)
下麵再計算XT50-K的預測結果。
根據XT50-K的銷售數據及公式(11) 、(14)、(17)、(18)、(19)有:
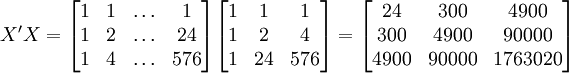 。
。
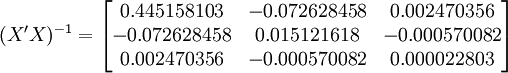
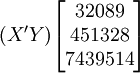
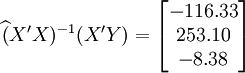
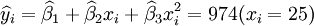
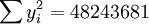 ;
;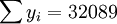 ;
;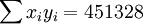 ;
;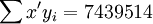
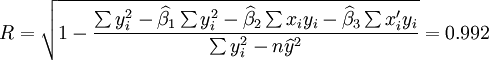
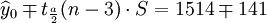 (t0.025(21) = 2.080)
(t0.025(21) = 2.080)
下麵再計算XT50—K的預測結果。
根據XT50---K的銷售數據及公式(11)、(14)、(17)、(18)、(19)有:
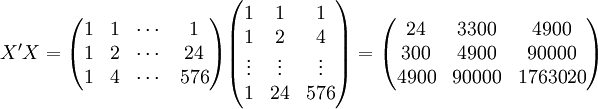
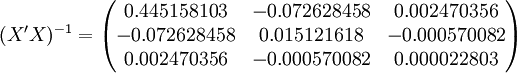
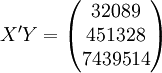
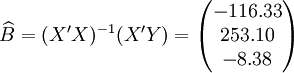
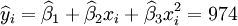 (xi = 25)
(xi = 25)
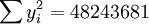 ;
;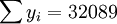 ;
;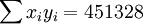 ;
;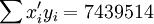
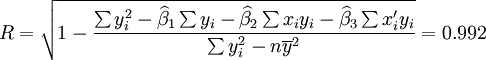
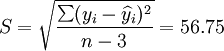
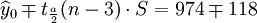 t0.025(21) = 2.080
t0.025(21) = 2.080
3.預測結果分析
從2001年第一季度的預測結果和實際值的比較來看,預測還算是可行的,XTl00—W和XT50—K的實際銷售量均在預測範圍之內,回歸繫數也都接近於1,說明這兩種車型選取非線性回歸的二次曲線模型還是比較合適的。但是,還應該看到,兩種車型的預測結果中估計標準差S都比較大,說明回歸曲線和實際銷售數據的擬合情況並不太好,而S數值的偏大同時也帶來了預測範圍較大的後果。因此,預測精度較差。
當然了,實際工作中不可能會有真正符合某條曲線的數據存在,只能是從散點圖來看大致符合某種曲線,就用該種曲線來進行擬合,以求大致的預測結果。因此,對於XTl00—W和XT50—K的預測還是可行的。
再進一步考慮,XTl00—W的預測值比實際值大了66,說明實際下降趨勢比預測的要小,而XT50—K的情況則剛好相反。如果排除偶然因素的話,有可能XTlOO—w銷售量的下降趨勢在減緩,而XT50—K則相反,下降趨勢在加劇。聯繫實際情況,作者認為是50車型的銷量因競爭的日益加劇和政策的影響而加速下滑,而100車型則可能是由於公司的努力而減低了銷量下降的速度。作者的這個想法在後來和新田公司總工程師匡建中的交流中得到了驗證。
(三)虛擬變數回歸預測法的運用
在回歸模型分析中,有時還要考慮諸如性別、文化程度、宗教、戰爭、災難、季節以及政府經濟政策變化等品質變數的影響。這時,可在建立回歸模型時將品質變數引入線性回歸模型中,這種回歸預測法就是虛擬變數回歸預測法。
常見的帶虛擬變數的回歸模型有以下三種形式:
(1)反映政府政策變化或某種因素髮生重大變異的跳躍、間斷式模型。
(2)具有轉折點的系統趨勢變化模型。
(3)含有多個虛擬變數的線性回歸模型。
虛擬變數回歸預測法的適用性一般在散點圖上明確看出。在表(1.1)中的數據都不適用。不過,作者發現新田公司的XT50—M在無錫的銷售倒是適合用具有轉折點的系統趨勢變化模型來進行預測。
1.預測模型
由於只有XT50—M在無錫的銷售適合用具有轉折點的系統趨勢變化模型來 進行預測(見是表4)下麵僅介紹具有轉折點的系統趨勢變化模型。
具有轉折點的系統趨勢變化模型為:
yi = β1 + β2xi + β3(xi − x0)Di + εi (21)
式中Di為虛擬變數,Di的取值為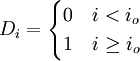
io為發生轉折點的時間,xo為io時間xi的觀察值。(21)可變形為:
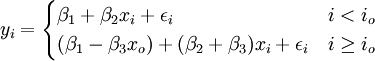
根據(21),可令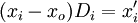 ,,則該虛擬變數回歸轉化為二元線性回歸,可用二元線性回歸的計算方法計算。
,,則該虛擬變數回歸轉化為二元線性回歸,可用二元線性回歸的計算方法計算。
2)預測計算
經過對散點圖觀察發現,1998年第四季度為轉折點,即i0 = 12,由表(4)的數據及(14)、(17)、(18)、(19)、(21)可得:
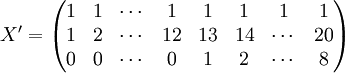
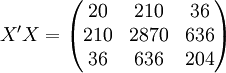
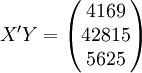
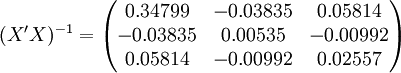
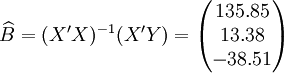
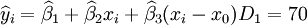 xi = 21
xi = 21
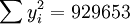 ;
;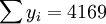 ;
;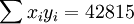 ;
;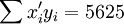
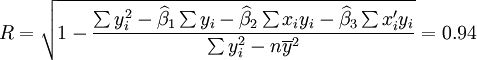
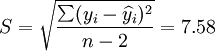
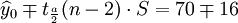 (t0.025(18) = 2.101)
(t0.025(18) = 2.101)
3.預測結果分析
新田公司的XT50—M2001年第一季度在無錫的實際銷售量為55輛,和預測結果相比,可以說還在預測範圍內,說明該車型在無錫的銷售用虛擬變數回歸預測法預測還是比較成功的。而之所以會在98年第四季度出現轉折點,作者還是瞭解的,原因就在於98年第四季度無錫市公佈了50車型不允許上助力車牌照的規定,從而引起了50車型在無錫的銷售量逐步減少。當然了,這種情況銷售預測中出現得不多,因此使用也不是很廣。
三、回歸分析法總結
回歸分析預測法是一類比較經典,也比較實用的預測方法。正是由於它經典,因此也就成熟,再加上比較容易理解,運用也就比較廣泛。相比之下,其中的線性回歸預測法和非線性回歸預測法的運用更廣些。在實際使用過程中,如果在選擇具體的方法和模型時能對數據作較為詳細的分析,對散點圖的觀察分析也能仔細一點的話,預測結果也就會比較令人滿意的。當然了回歸分析最大的特點就是在偶然中發現必然,而實際情況卻常常是千變萬化的,有時偶然因素的影響也會超過必然,這時預測結果也就不能很如意,這就要求在預測工作中不能機械,要會靈活運用,要註意瞭解會影響預測結果的偶然情況,以便對預測結果進行適當修正,這樣才能使預測結果更接近實際,也才能使預測能更好地為經濟建設服務。從新田公司的回歸分析預測結果來看,用線性回歸預測法來預測XTl50-T、XTl25—C和XTl25一W都得到了比較滿意的結果,而且各項指標也比較好,用虛擬變數回歸預測法預測XT50—M也得到了滿意的結果。因此可以基本上確定,用上述的預測方法來預測新田公司的這幾種車型是可行的。(參見下麵二圖)。
- ↑ 錢曉星.新田公司摩托車銷售預測研究[D].2002
本条目由以下用户参与贡献
sky,funwmy,Zfj3000,Angle Roh,Vulture,Dan,Jiangyingrong,Ljf0516,Yixi,Zxe,Boomtown,Landscape,Arran,林巧玲,Mis铭,essilco.評論(共37條)
已做了部分修改,希望對你有所幫助~~
MBA智庫百科是可以自由參與編輯和修改的百科,如有發現錯誤和不足,您也可以進行修改哦~
以前在書本上看過關於回歸分析法的講解,但從來沒想過怎麼用,原來這種方法運用的這麼廣,雖然計算過程還是沒看明白,但大體意思懂了,謝謝。
額。。。看的懂例子,看不懂數據。
股市的相關係數太多了,不合適做教學。
某次調查活動涉及的調查對象總體包括公務員5萬人,企業管理人員10萬人和教育人士7萬人,擬採用分層比例抽樣法從總體中抽取2000人作為調查樣本,公務員,企業管理人員和教育界人士和各應抽取多少人?
還是不明白,這些是大學里學的嗎?
要看你學得是不是統計學,這個是統計學知識








真是好文章