對數模型
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
對數模型(Logit Model)
目錄 |
[編輯]
對數模型的概述[1]
對數模型是將貸款者的違約概率限定在0和1之間,並且通過函數的對數分佈來計算違約的概率.
[編輯]
對數模型的數學表達式為:
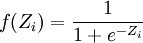
式中,e代表指數;
F(Zi)是貸款累積的違約概率;
Z是用與線性概率模型類似的方式通過回歸計算出來的。
從根本上講,我們運用與線性概率模型相同的方法,從回歸模型中估計出借款者的Z值,然後將其代入對數函數的右端,這就直接產生了F(Zi)值,它即為違約的概率。
[編輯]
對數模型的主要弱點是假設違約概率呈現出特定的對數函數形式。
[編輯]
- ↑ 龔明華編著. 現代商業銀行業務與經營. 中國人民大學出版社, 2006.03.







