修正持久期
出自 MBA智库百科(https://wiki.mbalib.com/)
修正久期(Modified duration)
目錄 |
什麼是修正持久期[1]
修正持久期是衡量價格對收益率變化的敏感度的指標。在市場利率水平發生一定幅度波動時,修正持久期越大的債券,價格波動越大(按百分比計)。
對於給定的到期收益率的微小變動,債券價格的相對變動與其麥考利久期成比例。當然,這種比例關係只是一種近似的比例關係,它的成立是以債券的到期收益率很小為前提的。為了更精確地描述債券價格對於到期收益率變動的靈敏性,又引入了修正久期模型(Modified Duration Model)。修正久期被定義為:
修正久期的定義:
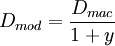
Dmac為麥考利久期
從這個式子可以看出,對於給定的到期收益率的微小變動,債券價格的相對變動與修正久期之間存在著嚴格的比例關係。所以說修正久期是在考慮了收益率項y的基礎上對 Macaulay久期進行的修正,是債券價格對於利率變動靈敏性的更加精確的度量。
修正久期大抵抗利率上升風險弱,抵抗利率下降風險能力強;久期小抵抗利率上升風險能力強,抵抗利率下降風險能力弱。
當我們判斷當前的利率水平存在上升可能,就可以集中投資於短期品種、縮短債券久期;而當我們判斷當前的利率水平有可能下降,則拉長債券久期、加大長期債券的投資,這就可以幫助我們在債市的上漲中獲得更高的溢價。
EXCEL可以通過財務函數中的MDURATION函數計算
- 債券的現行價格為所有各期未來現金流的現值的加總
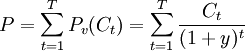
- 麥考利久期
![D_{mac}=\frac{\sum_{t=1}^T \left[t \bullet {\frac{C_t}{(1+y)^t}}\right]}{P}](/w/images/math/c/a/8/ca8c25f7403c9ab14b8679944e2c0959.png)
- 將債券價格公式看作P與1+y之間的函數,可以有
![\frac{dP}{d(1+y)}= -\sum_{t=1}^T\frac{t\bullet C_t}{(1+y)^{t+1}} =-\frac{1}{1+y}\bullet \sum_{t=1}^T \left[t \bullet {\frac{C_t}{(1+y)^t}}\right]](/w/images/math/d/0/3/d033258a693a5f853af869b9a6778133.png)
- 等式兩邊除以P
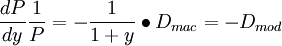
- 對於P和y的微小變化有:
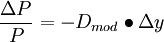
上式表明:債券價格變化的百分比恰好等於修正久期與債券到期收益率變化的乘積。因此,修正久期可以用來測度債券在利率變化時的風險暴露程度。
市場利率的波動是債券價格變動的主要原因。如果將債券的價格看成是市場利率的函數,記為,
PB = PB(i)
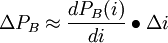
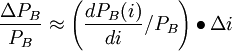
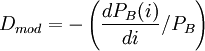
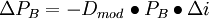
債券的價格的變化等於債券的修正久期乘以債券的價格再乘以市場利率的變化。久期實際描述的是債券價格對市場利率的一階導數關係;
修正持久期的計算[2]
- 修正久期的計算公式:
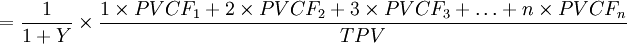
其中:
PVCFt為以t期對應的市場普遍收益率進行貼現得到的債券在第t期的現金流現值;
n為債券持有期內現金流的期間總數;
TPV為債券各期現金流的總現值;
Y為到期收益率的一半。
- 修正久期的近似計算
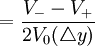
其中:
V − 為收益率下降△y證券的估計價格;
V + 為收益率上升△y證券的估計價格;
V0為證券初始價格;
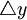 為證券收益率的變化。
為證券收益率的變化。
評論(共8條)
那個最後面的Y為什麼等於收益率的一半啊?不是就應該是收益率本身嗎?
我也認為應該是收益率的本身,不應該是收益率的一半
那個最後面的Y為什麼等於收益率的一半啊?不是就應該是收益率本身嗎?
是因為美國國債都是以半年付息的,我國記帳式國債,半年付息的一般是10年以上的長期國債,按一年付息一般是7年以下的中短期國債。








很詳細。有參考價值,謝謝。