修正持久期
出自 MBA智库百科(https://wiki.mbalib.com/)
修正久期(Modified duration)
目录 |
什么是修正持久期[1]
修正持久期是衡量价格对收益率变化的敏感度的指标。在市场利率水平发生一定幅度波动时,修正持久期越大的债券,价格波动越大(按百分比计)。
对于给定的到期收益率的微小变动,债券价格的相对变动与其麦考利久期成比例。当然,这种比例关系只是一种近似的比例关系,它的成立是以债券的到期收益率很小为前提的。为了更精确地描述债券价格对于到期收益率变动的灵敏性,又引入了修正久期模型(Modified Duration Model)。修正久期被定义为:
修正久期的定义:
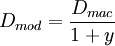
Dmac为麦考利久期
从这个式子可以看出,对于给定的到期收益率的微小变动,债券价格的相对变动与修正久期之间存在着严格的比例关系。所以说修正久期是在考虑了收益率项y的基础上对 Macaulay久期进行的修正,是债券价格对于利率变动灵敏性的更加精确的度量。
修正久期大抵抗利率上升风险弱,抵抗利率下降风险能力强;久期小抵抗利率上升风险能力强,抵抗利率下降风险能力弱。
当我们判断当前的利率水平存在上升可能,就可以集中投资于短期品种、缩短债券久期;而当我们判断当前的利率水平有可能下降,则拉长债券久期、加大长期债券的投资,这就可以帮助我们在债市的上涨中获得更高的溢价。
EXCEL可以通过财务函数中的MDURATION函数计算
- 债券的现行价格为所有各期未来现金流的现值的加总
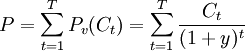
- 麦考利久期
![D_{mac}=\frac{\sum_{t=1}^T \left[t \bullet {\frac{C_t}{(1+y)^t}}\right]}{P}](/w/images/math/c/a/8/ca8c25f7403c9ab14b8679944e2c0959.png)
- 将债券价格公式看作P与1+y之间的函数,可以有
![\frac{dP}{d(1+y)}= -\sum_{t=1}^T\frac{t\bullet C_t}{(1+y)^{t+1}} =-\frac{1}{1+y}\bullet \sum_{t=1}^T \left[t \bullet {\frac{C_t}{(1+y)^t}}\right]](/w/images/math/d/0/3/d033258a693a5f853af869b9a6778133.png)
- 等式两边除以P
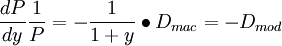
- 对于P和y的微小变化有:
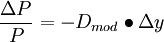
上式表明:债券价格变化的百分比恰好等于修正久期与债券到期收益率变化的乘积。因此,修正久期可以用来测度债券在利率变化时的风险暴露程度。
市场利率的波动是债券价格变动的主要原因。如果将债券的价格看成是市场利率的函数,记为,
PB = PB(i)
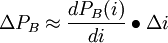
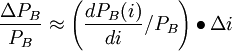
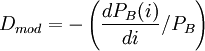
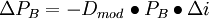
债券的价格的变化等于债券的修正久期乘以债券的价格再乘以市场利率的变化。久期实际描述的是债券价格对市场利率的一阶导数关系;
修正持久期的计算[2]
- 修正久期的计算公式:
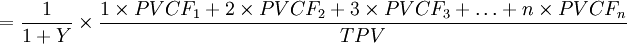
其中:
PVCFt为以t期对应的市场普遍收益率进行贴现得到的债券在第t期的现金流现值;
n为债券持有期内现金流的期间总数;
TPV为债券各期现金流的总现值;
Y为到期收益率的一半。
- 修正久期的近似计算
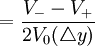
其中:
V − 为收益率下降△y证券的估计价格;
V + 为收益率上升△y证券的估计价格;
V0为证券初始价格;
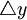 为证券收益率的变化。
为证券收益率的变化。
评论(共8条)
那个最后面的Y为什么等于收益率的一半啊?不是就应该是收益率本身吗?
我也认为应该是收益率的本身,不应该是收益率的一半
那个最后面的Y为什么等于收益率的一半啊?不是就应该是收益率本身吗?
是因为美国国债都是以半年付息的,我国记帐式国债,半年付息的一般是10年以上的长期国债,按一年付息一般是7年以下的中短期国债。








很详细。有参考价值,谢谢。