MNL模型
出自 MBA智库百科(https://wiki.mbalib.com/)
MNL模型(Multinominal Logit Model)
目錄 |
MNL是Logit類模型的基本型式,其效用隨機項εi,q 相互獨立且服從同-gumble極值分佈。基於概率理論,J個選擇項MNL模型可以表達成:
 i=1,2……J (1)
i=1,2……J (1)
Pi,q是出行者q對選擇項i的概率,b是參數。
MNL模型通過效用函數確定項的計算就可以獲得個體不同交通方式的選擇概率。通過模型標定,其效用函數的隨機項因素影響已經被表達在參數b中。
由於模型概念明確、計算方便而在經濟、交通等多方面得到廣泛應用。
MNL模型也在應用中受到某些制約,最大限制在於各種交通方式在邏輯上必須是對等的(IIA特性)。如果主要方式和次要方式混雜在一起,所得到的結果就會有誤差。MNL模型應用中表現的另一點不足是計算概率僅與交通方式效用項差值有關,而與效用值自身大小無關,缺乏方式之間的相對比較合理性。
產生限制或不足的根本原因是Logit模型在推導中假定了效用隨機項是獨立分佈的(IID:Independent and Identical Distribution),但在現實中存在著影響各選擇項效用的共同因素,組成效用項的某個因素髮生變化,會引發多種交通方式市場份額的變化,其影響大小可以引用經濟學中的交叉彈性繫數來表達。
現有MNL模型的改進中常用的有BCL模型(Box-Cox logit),NL(巢式)模型(Nested logit mode1),Dogit模型和BCD模型(Box-Cox Dogit)。
BCL模型對效用項計算進行變換,方式選擇概率計算與效用項的大小有了關聯,也改善了方式之間的合理可比性。
NL模型是對MNL的直接改進,它由交通方式的邏輯劃分、結構繫數與MNL子模型共同構成,由於各種方式之間明確了邏輯關係,子巢內交通方式選擇概率由結構繫數控制,因此它緩解了IIA問題,是目前應用最為廣泛的模型之一。但巢式層次結構的構造沒有一定的規則可循,方式劃分的不同帶來計算結果也不盡相同。
Dogit將交通方式選擇劃分為“自由選擇”與“強迫選擇”兩部分,“強迫選擇”方式是交通的基本必要消費(如上下班、上下學出行),“自由選擇”相對為非基本消費,且服從MNL模型。dogit模型比MNL模型減小了交叉彈性繫數,改變子選擇項數量對其他選擇枝的概率影響相應減小。此外,每個選擇項的交叉彈性繫數可以不同,使得選擇項之間的柔性增加。
BCD模型組合了BCL模型的效用確定項計算變換與Dogit模型,它同時完成了BCL和Dogit兩個模型從IIA到交叉彈性兩個方面的改進。
1.CNL模型(Cross-nested logit)
CNL模型(Voshva,1998)是MNL模型的又一改進模型,為了體現各選擇項之間的相關和部分可替代性,它設有m個選擇子巢,允許各選擇項按不同的比例分配到各個結構參數相同的選擇子巢中,其單一選擇項概率可表達為所有被選中的包含該選擇項的子巢概率和子巢內選擇該選擇項概率的乘積和:
![P_i=\sum_{m}P_{i/m}\cdot P_m=\sum_{m}\left[\frac{(\alpha_{im}e^{V_i})^{1/\theta}}{\sum_{j\in N_{m}}(\alpha_{jm}e^v_J)^{1/\theta}}\cdot\frac{\sum_{j\in N_{m}}(\alpha_{jm}e^v_J)^{1/\theta}}{\sum_{m}(\sum_{j\in N_{m}}(\alpha_{jm}e^v_i)^{1/\theta})^\theta}\right]](/w/images/math/0/6/8/0688e06516889a939a2d92966d6681ed.png) (2)
(2)
| ∑ | αim = 1 |
| m |
2. PCL模型(Paired combinatorial logit)和GNL模型(Generalized nested logit)
PCL模型(Chu,1989;Koppelman and Wen,2000)是展開形式的特殊巢式結構的CNL模型,它將選擇項兩兩組成對,選擇i項的概率即為所有與i項成對的對(也稱為子巢)選擇概率與對中i項選擇概率的乘積和:
![P_i=\sum_{J\ne1}P_{i/ij}\cdot P_{ij}=\sum_{j\ne1}\left\{\frac{(\alpha e^{V_i})^{1/\theta_{iJ}}}{(\alpha e^{V_i})^{1/\theta_{ij}}+(\alpha e^{V_J})^{1/\theta_{iJ}}}\cdot\frac{[(\alpha e^{V_{i}})^{1/\theta_{iJ}}+(\alpha e^V_{J})^{1/\theta_{iJ}]^\theta_{iJ}}}{\sum_{k=1}^{J-1}\sum_{m=k+1}^J[(\alpha e^{V_{k}})^{1/\theta_{km}}+(\alpha e^V_{m})^{1/\theta_{km}]^\theta_{km}}}\right\}](/w/images/math/6/1/8/618b4b89adf90d90edbf77a79f8901c4.png) (3)
(3)
其中,J為選擇項總數,θ∈(0,1)為每個對的結構參數,α=1/(j-1)為分配份額參數,表示i分配到(i,j)對的概率。由於模型子巢是選擇對,兩選擇項之間不同的交叉彈性、部分可替代性可以充分表達,從而進一步緩解了IIA特性。但相同的分配參數僅(這與CNL模型可任意比例分配不同),限制了交叉彈性繫數的最大值,也限制了最大相關。
如果改PCL結構參數0可變,結合CNL可變的選擇項分配份額參數僅,便組成具有充分“柔性”的GNL模型(Wen and Koppelman,2000),PCL和CNL模型是GNL模型的特例。
3.HMNL模型(Heteroscedastic muhinomial logit)和COVNL模型(Covariance heterogeneous nested logit)
HMNL模型(Swait and Adamowicz,1996)從另一個角度、由MNL模型發展而來,它保留了MNL模型的形式、IIA特性和同一的交叉彈性,但它允許效用隨機項之間具有相異方差,它認為不同出行者對效用的感受能力和應對方法是不同的,這種不同可以通過隨機效用項異方差表達在模型中。不同於MNL,HMNL認為,不同的出行者感受到的選擇項集合與選擇分類方式是不完全相同的,因此效用可觀測項定義為與選擇項i和整個被選擇的交通系統劃分方式q (即方式選擇的樹形結構)有關的函數。
Eq為個人特性(如收入)與被選擇系統(如選擇項數量、選擇項之間的相似程度)的函數。尺度因數μ(Eq)是表達交通系統組成(樹形結構)複雜程度的函數。由於計算概率值受到尺度因數的控制,各選擇項之間就具有了不同相關關係與部分可替代的“柔性”:
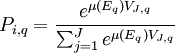 (4)
(4)
HMNL模型定義的尺度因數可以確保不同出行者所感受到的不盡相同的交通系統的選擇項之間有不同的交叉彈性和相關性。
COVNL模型(Bhat,1997)是一種擴展的巢式模型,它在選擇巢之間允許有不同方差,通過結構繫數函數化以達到選擇巢之間的相關性和部分可替代性的目的:
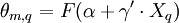 (5)
(5)
式中,結構繫數 ,F是傳遞函數,Xq是個人和交通相關的特性向量,α和
,F是傳遞函數,Xq是個人和交通相關的特性向量,α和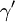 是需要估計的參數,可根據經驗給定。從模型各選擇項的可變的交叉彈性繫數(
是需要估計的參數,可根據經驗給定。從模型各選擇項的可變的交叉彈性繫數(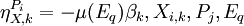 可變,交叉彈性可變)可以看出,選擇項之間可以存在不同相關關係與柔性的部分可替代性。如果
可變,交叉彈性可變)可以看出,選擇項之間可以存在不同相關關係與柔性的部分可替代性。如果 ,則COVNL模型退化為NL模型。
,則COVNL模型退化為NL模型。
一般認為,MNL模型隱含了三個假定:效用隨機項獨立且服從同一極值分佈(IID);各選擇項之間具有相同不變的交叉響應;效用隨機項間相同方差。這三項假定均不符合交通方式選擇的實際情況,並引發一些謬誤。MNL模型正是通過改善模型相對比較合理性,緩解或解除一個或多個隱含假定而發展起來的,其改進方法主要包括:
其一是對效用可觀測項計算進行非線性變換,改善單個因素對可觀測效用的邊際影響,提高各選擇項計算概率的相對比較合理性,BCL模型屬於此類型;另一種途徑是選擇項採用“市場競爭”的思想進行分類與份額分配,從而達到緩解IIA特性的目的,此類型包括Dogit和BCD模型等。
其二是建立“柔性模型結構”,它通過建立樹型巢式結構、定常或非定常的結構參數以及各選擇項分配到各子巢的份額參數,松馳了效用隨機項服從同一分佈和相互獨立性,同時也使得各選擇項交叉響應特性按分配差異產生變化。此類模型有NL、CNL、PCL和GNL模型以及其他的改進型:GenMNL(generalized MNL,Swait,2000)模型(分配參數不可變的GNL模型);FNL(fuzzy nest logit,Voshva,1999)模型(允許多級子巢嵌套的GNL模型);OGEV fordered generalized extreme value,Small,1987)模型(將部分可替代性好的選擇項分配到同一子巢中,通過改變同一個子巢中選擇項的數目、每個子巢中各選擇項分配份額和每個子巢的結構參數。達到各選擇項之間不同水平相關、部分可替代的目的);PD (principles of differentiation,Bresnahanet aI.1997)模型[認為同一類相近性質選擇項之間的競爭遠大於不同類選擇項之間的競爭,模型依循多種因素定義了類(子巢),並依循每種因素定義了多級水平。它不同於NL模型的有序樹形結構,是從一個有別於其他模型的角度建立樹形巢結構,允許不同因素的交叉彈性]。
其三是將各選擇項效用隨機項之間或選擇子巢之間異方差化來改善IIA引發的問題,HMNL和COVNL模型屬於此類型。








第一個公式應該是J不等於i