MNL模型
出自 MBA智库百科(https://wiki.mbalib.com/)
MNL模型(Multinominal Logit Model)
目录 |
MNL是Logit类模型的基本型式,其效用随机项εi,q 相互独立且服从同-gumble极值分布。基于概率理论,J个选择项MNL模型可以表达成:
 i=1,2……J (1)
i=1,2……J (1)
Pi,q是出行者q对选择项i的概率,b是参数。
MNL模型通过效用函数确定项的计算就可以获得个体不同交通方式的选择概率。通过模型标定,其效用函数的随机项因素影响已经被表达在参数b中。
由于模型概念明确、计算方便而在经济、交通等多方面得到广泛应用。
MNL模型也在应用中受到某些制约,最大限制在于各种交通方式在逻辑上必须是对等的(IIA特性)。如果主要方式和次要方式混杂在一起,所得到的结果就会有误差。MNL模型应用中表现的另一点不足是计算概率仅与交通方式效用项差值有关,而与效用值自身大小无关,缺乏方式之间的相对比较合理性。
产生限制或不足的根本原因是Logit模型在推导中假定了效用随机项是独立分布的(IID:Independent and Identical Distribution),但在现实中存在着影响各选择项效用的共同因素,组成效用项的某个因素发生变化,会引发多种交通方式市场份额的变化,其影响大小可以引用经济学中的交叉弹性系数来表达。
现有MNL模型的改进中常用的有BCL模型(Box-Cox logit),NL(巢式)模型(Nested logit mode1),Dogit模型和BCD模型(Box-Cox Dogit)。
BCL模型对效用项计算进行变换,方式选择概率计算与效用项的大小有了关联,也改善了方式之间的合理可比性。
NL模型是对MNL的直接改进,它由交通方式的逻辑划分、结构系数与MNL子模型共同构成,由于各种方式之间明确了逻辑关系,子巢内交通方式选择概率由结构系数控制,因此它缓解了IIA问题,是目前应用最为广泛的模型之一。但巢式层次结构的构造没有一定的规则可循,方式划分的不同带来计算结果也不尽相同。
Dogit将交通方式选择划分为“自由选择”与“强迫选择”两部分,“强迫选择”方式是交通的基本必要消费(如上下班、上下学出行),“自由选择”相对为非基本消费,且服从MNL模型。dogit模型比MNL模型减小了交叉弹性系数,改变子选择项数量对其他选择枝的概率影响相应减小。此外,每个选择项的交叉弹性系数可以不同,使得选择项之间的柔性增加。
BCD模型组合了BCL模型的效用确定项计算变换与Dogit模型,它同时完成了BCL和Dogit两个模型从IIA到交叉弹性两个方面的改进。
1.CNL模型(Cross-nested logit)
CNL模型(Voshva,1998)是MNL模型的又一改进模型,为了体现各选择项之间的相关和部分可替代性,它设有m个选择子巢,允许各选择项按不同的比例分配到各个结构参数相同的选择子巢中,其单一选择项概率可表达为所有被选中的包含该选择项的子巢概率和子巢内选择该选择项概率的乘积和:
![P_i=\sum_{m}P_{i/m}\cdot P_m=\sum_{m}\left[\frac{(\alpha_{im}e^{V_i})^{1/\theta}}{\sum_{j\in N_{m}}(\alpha_{jm}e^v_J)^{1/\theta}}\cdot\frac{\sum_{j\in N_{m}}(\alpha_{jm}e^v_J)^{1/\theta}}{\sum_{m}(\sum_{j\in N_{m}}(\alpha_{jm}e^v_i)^{1/\theta})^\theta}\right]](/w/images/math/0/6/8/0688e06516889a939a2d92966d6681ed.png) (2)
(2)
| ∑ | αim = 1 |
| m |
2. PCL模型(Paired combinatorial logit)和GNL模型(Generalized nested logit)
PCL模型(Chu,1989;Koppelman and Wen,2000)是展开形式的特殊巢式结构的CNL模型,它将选择项两两组成对,选择i项的概率即为所有与i项成对的对(也称为子巢)选择概率与对中i项选择概率的乘积和:
![P_i=\sum_{J\ne1}P_{i/ij}\cdot P_{ij}=\sum_{j\ne1}\left\{\frac{(\alpha e^{V_i})^{1/\theta_{iJ}}}{(\alpha e^{V_i})^{1/\theta_{ij}}+(\alpha e^{V_J})^{1/\theta_{iJ}}}\cdot\frac{[(\alpha e^{V_{i}})^{1/\theta_{iJ}}+(\alpha e^V_{J})^{1/\theta_{iJ}]^\theta_{iJ}}}{\sum_{k=1}^{J-1}\sum_{m=k+1}^J[(\alpha e^{V_{k}})^{1/\theta_{km}}+(\alpha e^V_{m})^{1/\theta_{km}]^\theta_{km}}}\right\}](/w/images/math/6/1/8/618b4b89adf90d90edbf77a79f8901c4.png) (3)
(3)
其中,J为选择项总数,θ∈(0,1)为每个对的结构参数,α=1/(j-1)为分配份额参数,表示i分配到(i,j)对的概率。由于模型子巢是选择对,两选择项之间不同的交叉弹性、部分可替代性可以充分表达,从而进一步缓解了IIA特性。但相同的分配参数仅(这与CNL模型可任意比例分配不同),限制了交叉弹性系数的最大值,也限制了最大相关。
如果改PCL结构参数0可变,结合CNL可变的选择项分配份额参数仅,便组成具有充分“柔性”的GNL模型(Wen and Koppelman,2000),PCL和CNL模型是GNL模型的特例。
3.HMNL模型(Heteroscedastic muhinomial logit)和COVNL模型(Covariance heterogeneous nested logit)
HMNL模型(Swait and Adamowicz,1996)从另一个角度、由MNL模型发展而来,它保留了MNL模型的形式、IIA特性和同一的交叉弹性,但它允许效用随机项之间具有相异方差,它认为不同出行者对效用的感受能力和应对方法是不同的,这种不同可以通过随机效用项异方差表达在模型中。不同于MNL,HMNL认为,不同的出行者感受到的选择项集合与选择分类方式是不完全相同的,因此效用可观测项定义为与选择项i和整个被选择的交通系统划分方式q (即方式选择的树形结构)有关的函数。
Eq为个人特性(如收入)与被选择系统(如选择项数量、选择项之间的相似程度)的函数。尺度因子μ(Eq)是表达交通系统组成(树形结构)复杂程度的函数。由于计算概率值受到尺度因子的控制,各选择项之间就具有了不同相关关系与部分可替代的“柔性”:
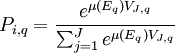 (4)
(4)
HMNL模型定义的尺度因子可以确保不同出行者所感受到的不尽相同的交通系统的选择项之间有不同的交叉弹性和相关性。
COVNL模型(Bhat,1997)是一种扩展的巢式模型,它在选择巢之间允许有不同方差,通过结构系数函数化以达到选择巢之间的相关性和部分可替代性的目的:
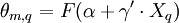 (5)
(5)
式中,结构系数 ,F是传递函数,Xq是个人和交通相关的特性向量,α和
,F是传递函数,Xq是个人和交通相关的特性向量,α和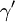 是需要估计的参数,可根据经验给定。从模型各选择项的可变的交叉弹性系数(
是需要估计的参数,可根据经验给定。从模型各选择项的可变的交叉弹性系数(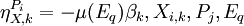 可变,交叉弹性可变)可以看出,选择项之间可以存在不同相关关系与柔性的部分可替代性。如果
可变,交叉弹性可变)可以看出,选择项之间可以存在不同相关关系与柔性的部分可替代性。如果 ,则COVNL模型退化为NL模型。
,则COVNL模型退化为NL模型。
一般认为,MNL模型隐含了三个假定:效用随机项独立且服从同一极值分布(IID);各选择项之间具有相同不变的交叉响应;效用随机项间相同方差。这三项假定均不符合交通方式选择的实际情况,并引发一些谬误。MNL模型正是通过改善模型相对比较合理性,缓解或解除一个或多个隐含假定而发展起来的,其改进方法主要包括:
其一是对效用可观测项计算进行非线性变换,改善单个因素对可观测效用的边际影响,提高各选择项计算概率的相对比较合理性,BCL模型属于此类型;另一种途径是选择项采用“市场竞争”的思想进行分类与份额分配,从而达到缓解IIA特性的目的,此类型包括Dogit和BCD模型等。
其二是建立“柔性模型结构”,它通过建立树型巢式结构、定常或非定常的结构参数以及各选择项分配到各子巢的份额参数,松驰了效用随机项服从同一分布和相互独立性,同时也使得各选择项交叉响应特性按分配差异产生变化。此类模型有NL、CNL、PCL和GNL模型以及其他的改进型:GenMNL(generalized MNL,Swait,2000)模型(分配参数不可变的GNL模型);FNL(fuzzy nest logit,Voshva,1999)模型(允许多级子巢嵌套的GNL模型);OGEV fordered generalized extreme value,Small,1987)模型(将部分可替代性好的选择项分配到同一子巢中,通过改变同一个子巢中选择项的数目、每个子巢中各选择项分配份额和每个子巢的结构参数。达到各选择项之间不同水平相关、部分可替代的目的);PD (principles of differentiation,Bresnahanet aI.1997)模型[认为同一类相近性质选择项之间的竞争远大于不同类选择项之间的竞争,模型依循多种因素定义了类(子巢),并依循每种因素定义了多级水平。它不同于NL模型的有序树形结构,是从一个有别于其他模型的角度建立树形巢结构,允许不同因素的交叉弹性]。
其三是将各选择项效用随机项之间或选择子巢之间异方差化来改善IIA引发的问题,HMNL和COVNL模型属于此类型。








第一个公式应该是J不等于i