跨期資本資產定價模型
出自 MBA智库百科(https://wiki.mbalib.com/)
跨期資本資產定價模型(Intertemporal Capital Asset Pricing Model 或 Intertemporal CAPM,簡稱ICAPM),也稱瞬時資本資產定價模型
在資產定價理論中的另一個重要假設是:證券市場總是在連續過程中,在這一假設前提下,Merton(1969,1971)將CAPM發展為跨期資本資產定價模型(ICAPM),同樣在信息對稱、無摩擦的市場中,資產價格的變化符合Ito過程,在這種條件下,資產的價格與投資者的效用偏好無關。在隨後的研究中Merton(1973)和Black(1973)應用以上連續時間模型成功地得到了期權定價公式,這一公式後來被大量的實證研究所證實,並且被廣泛在實踐中應用。
傳統CAPM中的一個關鍵假設是投資者只考慮單一投資期,很顯然這是一個不現實的假設。為了放鬆這一假設,把CAPM模型擴展到動態環境中,默頓(1969,1972,1973)構建了一個連續時間的投資組合與資產定價的理論框架,提出了一個跨期CAPM (ICAPM)。
默頓認為,投資者對風險證券的需求包括兩部分:馬科維茨的靜態資產組合最優化問題中的均值一方差成分和規避對投資機會集的不利衝擊的需求。當投資機會集發生不利變動,而同時又存在一種收益率很高的證券時,每一個理性的投資者都會希望買入該種證券作為一種套期保值措施。這種套期保值需求的增加同時也導致了該證券均衡價格的升高,推導ICAPM的關鍵就是在資產定價方程中反映這種套期保值需求。
![max E \left[ \int_{0}^{T} U^k (C^k (t))e^{- \rho ^{k}t}dt + U^k (W^k(T))e^{-\rho^{k}T} | \Omega_{0}\right]](/w/images/math/9/6/c/96c09507368482ab88c25cb130ccbbb2.png)
其中,U^k表示投資者k的效用,C^k表示投資者k的消費,\rho表示未來效用的貼現因數。第一項表示從0到T期的消費效用的現值,第二項表示在T期末財富效用的現值。
按照動態規劃原理,求解上述最大化問題需要確定每一期的消費量Ck(t)和餘下財富投資於每一資產的比重Wk(t)ni=1。為此,定義一個性能函數Jk(Wk,t,X)為:
![J^k(W^k,t,X)=max E \left[ \int_{t}^{T} U^k (C^k(t))e^{-\rho^{k}}z dt + U^k(W^K(t))e^{-\rho^{k}t}| \Omega_{t} \right]](/w/images/math/f/a/c/fac007bde460f27a37f705ff68123966.png)
利用高等數學和隨機微分知識,可求得(n+1)個最大化的一階條件,由此可以確定投資者在每一期的消費和投資組合變數。進一步地,默頓提出了類似於托賓分離定理的"(m+2)基金定理"(其中,m表示狀態變數個數)。他認為投資者應該持有(m+2)個資產組合:(1)最優風險證券組合,即切點組合;(2)無風險資產組合;(3)與某一狀態變數高度負相關的資產構成的其他m個資產組合(即套期保值組合)。前兩個資產組合確保投資者持有均值方差有效的資產組合,即位於靜態CAPM的有效邊界上,後m個資產組合則是為規避投資機會集的不利變動。
對所有投資者的需求方程加總,利用均衡狀態下總需求等於所有資產的總價值的基本原理,最終可推導出跨期資本資產定價模型ICAPM:
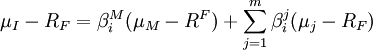
在ICAPM中,即使β值為零的資產,即與市場組合不相關的資產,其收益率也可能高於無風險利率,因為還需補償狀態變數的不利變動風險暴露。








very good