逆向歸納法

出自 MBA智库百科(https://wiki.mbalib.com/)

逆向歸納法(backward induction)是求解動態博弈均衡的方法

　　逆向歸納法(backward induction)是求解動態博弈均衡的方法。所謂動態博弈是指博弈參與人的行動存在著先後次序，並且後行動的參與人能夠觀察到前面的行動。逆向歸納法在邏輯上是嚴密的，然而它存在著“困境”。所謂逆向歸納法是從動態博弈的最後一步往回推，以求解動態博弈的均衡結果。逆向歸納法又稱逆推法。它是完全歸納推理，其推理是演繹的，即結論是必然的。^[1]

　　在完全且完美的動態博弈中，先行為的理性博弈人，在前面階段選擇策略時，必然會考慮後行博弈人在後面階段中將會怎樣選擇策略。因而，只有在博弈的最後一個階段，不再有後續階段牽制的情況下，博弈人才能作出明智的選擇。在後面階段博弈人選擇的策略確定後，前一階段的博弈人在選擇策略時也就相對容易。

　　逆向歸納法就是從動態博弈的最後一個階段開始分析，逐步向前歸納出各階段博弈人的選擇策略。

　　逆向歸納法的邏輯基礎：動態博弈中先行動的參與人，在前面階段選擇行為時必然會考慮後行動的參與人在後面階段中的行為選擇，只有在最後一階段的參與人才能不受其他參與人的制約而直接做出選擇。而當後面階段的參與人的選擇確定後，前一階段的參與人的行為也就容易確定了。逆向歸納法排除了不可信的威脅或承諾。

　　逆向歸納法：它的精髓就是“向前展望，向後推理”，即首先仔細思考自己的決策可能引起的所有後續反應，以及後續反應的後續反應，直至博弈結束；然後從最後一步開始，逐步倒推，以此找出自己在每一步的最優選擇。^[1]

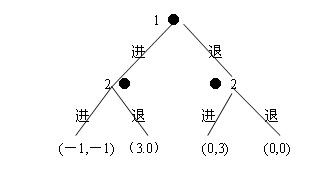
　　圖1的求解過程如下：

（a）若2在右，2將選擇進（0.3）；∵（0.3）＞（0.0）

（b）若2在左，2將選擇退（3.0）；∵（3.0）＞（-1.-1）

（c）在2的選擇中1的最大收益是選擇進；∵（3.0）＞（0.3）

∴納什均衡為（進（進，退））均衡解為（進，退），均衡收益為（3.0）

　　（2）逆向歸納法僅適合有限步動態博弈，而且要求決策者犯的可能性很小。

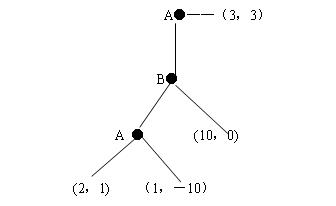
　　如果使用逆向歸納法得到的結果是A選擇右邊的行動，雙方各得3。

　　如果A在第一步選擇下邊的行動，B該做何想？只有當A在第二步犯錯誤的可能性小於1/11時，B才有膽量選擇讓游戲繼續玩下去。於是A極有可能獲得10這個最大回報。

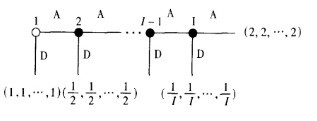
　　右圖所描述的I個參與人的博弈，在這裡，每一個參與人i<I可以選擇“D”來結束博弈，或者選擇“A”把採取行動的權利讓給參與人i+I。如果參與人i選擇了行動D，每一個參與人都能得到l／i；如果所有參與人都選擇了行動A，那麼每一個參與人都能得到2。

　　由於每次只有一個參與人採取行動，這是一個完美信息博弈，我們可以應用逆向歸納方法。用這一方法可以預測得每一個參與人應該都會選擇行動A。如果I很小，這似乎是一個合理的預測。如果I很大，那麼作為參與人1，我們自己將都會選擇D而不是A，其原因類似於獵鹿博弈中推導無效率均衡所用到的“穩健性”。

　　首先，收益2要求所有I—1個其他參與人都要選擇行動A。如果一個給定參與人選擇行動A的概率是P<l，並且與其他參與人的選擇是相互獨立的，那麼所有其他I-1個參與人都選擇行動A的概率就是p^{I − 1}，這一概率是很小的(即使p很大)。其次，我們會擔心參與人2可能也會有著同樣的考慮；也就是說，參與人2可能會選擇D，以防未來參與人出現“失誤”或者參與人3故意選擇D的可能。

　　一個相關結論是逆向歸納的鏈條越長，則其所假定的前提假設的鏈條也就越長(“參與人1知道參與人2知道參與人3知道……的收益”)。如果在圖中，I=2，逆向歸納假設參與人1知道參與人2的收益，或者至少參與人1充分地相信參與人2的最優選擇是A。如果I=3，不僅參與人l和參與人2瞭解參與人3的收益，而且參與人1還必須知道參與人2清楚參與人3的收益，從而參與人l可以預測參與人2對參與人3的行動預測，如果參與人1認為參與人2將會不正確地預測參與人3的行動選擇，那麼參與人1就會選擇行動D。習慣上，均衡分析是建立在收益作為一種“共同知識”的前提上的．從而任意長的“i知道j知道k知道”是有效的，但比起需要稍弱的共同知識前提假設所得列的結論，由這種形式的非常長鏈所得到的結論似乎更不合理(部分原因足由於逆向歸納的鏈條越長，就會對博弈信息結構的微小變化越敏感。)

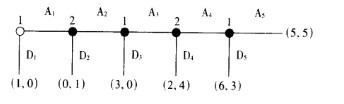
　　在右上圖所示的例子中，如果I非常大的話，那這一博弈就變得極為麻煩了。當同—個參與人可以接連幾次採取行動時，就會出現逆向歸納法中的第二個難點。考察右圖所示的博弈。在這裡，逆向歸納法的解就是採取行動參與人在每一個信息集上都採取行動D。這一解是否具有說服力呢？設想你就是參與人2；設想，與原來的預期相反，參與人1在他初次採取行動時選擇了行動A₁，你將會怎樣行動呢？逆向推理法表明你應選擇行動D₂，因為若給予參與人l下一次機會時他將選擇D₃；然而，逆向歸納法也表明參與人1本應是選擇D₁。

　　在這一博弈中，參與人2在參與人l偏離了其所預測的行動選擇A₁時，參與人2的最優選擇取決於自己如何認為參與人1在未來的行動：若參與人2認為存在至少25％的可能性參與人1會選擇行動A₃，則參與人2應選擇行動A₂。參與人2又是如何形成這些信念，並且到底什麼信念才是合理的呢?尤其是，與逆向歸納法相反，如果參與人1決定選擇行動A₁，那麼參與人2將應怎樣去預測參與人1的行動?在某些文章的討論中，選擇行動A₂似乎是一個有利可圖的賭博。

　　在經濟學文獻中，大部分的動態博弈分析仍然是毫無保留地使用逆向歸納法及其精煉，但近來對這一點持有懷疑態度的人多了起來。在右圖中所示的博弈是基於羅森泰爾(Rosenthal，1981)的例子，他是首先對逆向歸納法的邏輯性提出質疑的人之一。貝蘇(Basu，1988，1998)，鮑那諾(Bonanno，1988)，賓默爾(Binmore，1987，]988)以及倫尼(Reny，1986)論證，合理的博弈理產不應該在理論給定為0概率的事件發生時就排除行動選擇，因為理論並沒有給參與人提供在這些事發生的條件下如何建立他們預測的途徑。弗登博格、克瑞普斯和萊維的研究建議參與人把意外的偏離解釋成由於收益與原來所認定最有可能的情況發生偏差。因為任何博弈結果都可以解釋為對競爭對手收益的某種確認，這種方法就迴避了再零概率事件發生時如何形成信念的困難，它把發生“偏離”後如何去預測博弈問題改變為在給定觀察到的行動下哪—個另類收益是最可能的問題。弗登博格與克瑞普斯把它進一步擴展上升為一種方法論：他們論證任何博弈理論應該在某種意義上是“完備”的，即給任何可能的博弈行動賦予嚴格正的概率。運用這一理輪，參與人對後面博弈的條件預測總是有定義的。

　　收益不確定性不是建立一個完備理論的惟一方法。第二類方法是把任何擴展式博弈解釋為隱含參與人有時會犯一些小“錯誤”或“顫抖”(如澤爾滕1975提出的)。如澤爾滕所假設的，如果在不同信息集上“顫抖”的概率是相互獨立的，那麼無論過去多麼頻繁出現與逆向歸納法預測不符的情況，參與人都應繼續在當前子博弈中運用逆向歸納法來預測博弈行動，因此，把偏離用“顫抖”來解釋是一種為逆向歸納法辯護的方法。與之相關的問題是，參與人在多大程度上會把這種對偏離的“顫抖”解釋看做是反對其他理論解釋的依據。在右圖2中，如果參與人2觀察到A₁，那麼他(或她)應該把這種情況解釋為一種“顫抖”，還是看做參與人1將會選擇A₃種信號呢?

　　海盜分贓逆向歸納法的經典例子，其原型來自I．Stewart在《科學美國人》雜誌上的一篇文章《凶殘海盜的邏輯》。這個例子曾經被作為微軟公司招募員工的面試題目，你也可以嘗試著可以在幾分鐘之內求解出正確答案。

　　1.故事模型

　　話說有5個海盜搶來了100枚金幣，大家決定分贓的方式是：由海盜一提出一種分配方案，如果同意這種方案的人達到半數，那麼該提議就通過並付諸實施；若同意這種方案的人未達半數，則提議不能通過且提議人將被扔進大海喂鯊魚，然後由接下來的海盜繼續重覆提議過程。假設每個海盜都絕頂聰明，也不相互合作，並且每個海盜都想儘可能多得到金幣，那麼，第一個提議的海盜將怎樣提議既可以使得提議被通過又可以最大限度得到金幣呢?

　　我曾好幾次在學生中做過調查，如果他們就是第一個海盜會怎麼分。答案五花八門，但是大多數是表示平均分(每人20顆)——這可能是現實中的情況，公平觀念在博弈中發揮著作用。但是標準博弈論是研究人們完全理性的情況下極端複雜的策略互動後果，這裡的平均分配並不符合標準博弈論的邏輯。

　　那麼答案究竟是什麼呢?使用逆向歸納法可以求解如下：

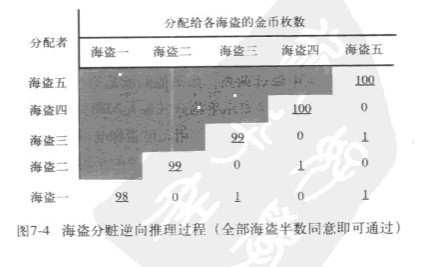
• 首先，考慮只剩下最後的海盜五，顯然他會分給自己100枚，並贊成自己。
• 再回溯到只剩下海盜四和海盜五的決策，海盜四可以分給自己100枚並贊成自己；海盜五被分得0枚，即使反對也無用。
• 回到海盜三，海盜三可以分給海盜五l枚得到海盜五的同意；分給自己99枚，自己也同意；分給海盜四0枚，海盜四反對但無用。
• 回到海盜二，海盜二可以分給海盜四1枚得到海盜四同意；分給自己99枚，自己也同意；海盜三、五各分得0枚，他們會反對但反對沒有用。
• 回到海盜一，他可以分給海盜三、五各l枚，獲得海盜三、五的同意；分給自己98，自己也同意；分給海盜二、四各0枚，他們會反對但反對不起作用。

　　因此，這個海盜分贓問題的答案是(98，0，1，0，1)：海盜一提出分給自己98枚，分給海盜二、四各0枚，分給三、五各1枚，該提議會被通過，因為海盜一、三、五會投贊成票。我們可以把這個逆向決策的過程用如下矩陣表達出來(如上圖，其中畫下劃線的數字表示海盜對該方案投了贊成票，未加下劃線對應於反對票)。

　　如果你是海盜一，你會這樣提方案嗎?

　　對於上述海盜分贓問題，我們還可以演化出不同的版本。比如說：(1)如果要求包括提議海盜在內的所有海盜過半數(超過1／2)同意才能使提議通過，那麼海盜一應該怎麼提方案?(2)如果要求提議海盜之外的海盜過半數同意才能通過，那麼海盜一又該怎麼提方案?(3)或者海盜的數目增加到10個、100個，海盜一又怎麼提方案?大家可以把這個當做練習題來做一做。

　　答案：變種問題(1)中，海盜一一提出的分配方案是(97，0，1，2，0)或(97，0，1，0，2)；變種問題(2)中，海盜一提出的分配方案應是(97，0，1，1，1)；變種問題(3)中，大家可嘗試逐漸增加海盜的數量，將會發現答案是有規律可循的。