子博弈

出自 MBA智库百科(https://wiki.mbalib.com/)

子博弈（Subgame）

　　子博弈是指在動態博弈中，所有參與人先後都採取了一次行動後所構成的一組新的博弈，這組博弈中的每一個都稱為“子博弈”。當只當參與人的戰略在其子博弈的系列（第二代、第三代…）中，每一個子博弈都構成納什均衡，就構成了子博弈精練納什均衡。

1、子博弈必須始於單個節點；

2、子博弈包含上述節點之後所有後續節點；

3、子博弈的信息集明確，不破壞任何信息集的完整性。即，信息集必須是完整的！

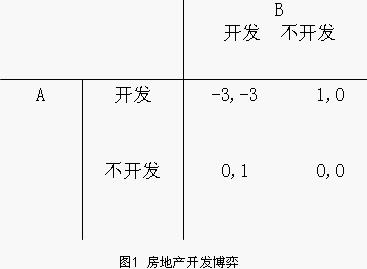
　　子博弈是原博弈的一部分，它本身可以作為一個獨立的博弈進行分析。例如圖1中，每一列或每一行都是一個子博弈，任何博弈本身則被稱為自身的一個子博弈。在A先採取行動後，B對A的回應構成包括原博弈在內的三個子博弈。

　　房地產開發商A是先行動者。在行動之前，A對競爭者B的戰略進行了預測，認為B有四種戰略可選：

• 無論A是否開發，B都要開發；
• 如果A開發，B也開發；如果A不開發，B也不開發。
• 如果A開發，B就不開發；如果A不開發，B就開發。
• 無論A是否開發，B必定不開發。

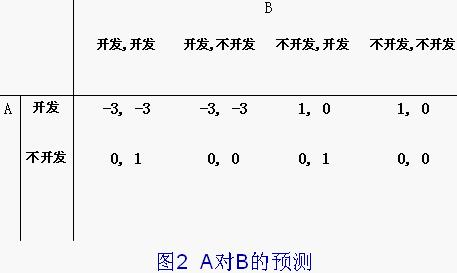
　　將B可能採取的戰略與圖1中博弈雙方相應選擇的得失結合起來，可以得出下圖。

　　在圖2中，存在著兩個納什均衡，即（A開發，B不開發）和（A不開發，B開發），而在B可能選擇的戰略中：

• 戰略1雖然包括了上述後一種納什均衡，但沒有包括前一種納什均衡；
• 戰略4雖然包括了上述前一種納什均衡，但沒有包括後一種納什均衡；
• 戰略2則上述兩種納什均衡都沒有包括；
• 只有戰略3包括了上述兩種均衡。

　　換句話說，如果B選擇戰略3，那麼不論A作出什麼選擇，B的回應都達到納什均衡，而在給定B會採取戰略3來回應A的選擇的前提下，開發是A的最優策略，因而A選擇了開發。

　　以上的分析方法，稱為子博弈精煉納什均衡。只有當某一戰略選擇在每一個子博弈（包括原博弈）上都構成一個納什均衡時，這一戰略組合才是子博弈精煉納什均衡。

　　而前面提到的B的四種戰略中，只有戰略3在所有子博弈中都構成納什均衡，所有這一博弈中唯一的子博弈精煉納什均衡，就是（開發，（不開發，開發）），即作為後行動者的B選擇戰略3，而作為先行動者的A選擇開發。

　　註：在A選擇開發時，無論B選擇戰略3或戰略4，其結果都構成納什均衡，而子博弈精煉納什均衡法要剔除的，正是這種在特定情況下是合理的，而在其他情況下不合理的戰略組合。