費馬大定理
出自 MBA智库百科(https://wiki.mbalib.com/)
費馬大定理(Fermat's Last Theorem)
目錄 |
費馬大定理也稱費馬最後定理(Le dernier théorème de Fermat),乃下述定理:
當整數n > 2時,關於x, y, z的不定方程:
xn + yn = zn.的整數解都是平凡解,即:
當n是偶數時:(0,±m,±m)或(±m,0,±m)
當n是奇數時:(0,m,m)或(m,0,m)或(m,-m,0)
這個定理,本來又稱費馬猜想﹝Fermat's conjecture﹞,由17世紀法國數學家皮埃爾·德·費馬提出。費馬在一本書的空位里寫,他已找到一個絕妙證明,但書邊沒有足夠的空位寫下。但經過三個半世紀的努力,這個世紀數論難題才由普林斯頓大學英國數學家安德魯·懷爾斯(Andrew Wiles)和他的學生理查·泰勒(Richard Taylor)於1995年成功證明。證明利用了很多新的數學,包括代數幾何中的橢圓曲線和模形式,以及伽羅華理論和Hecke代數等,令人懷疑費馬是否真的找到了正確證明。而安德魯·懷爾斯由於成功證明此定理,獲得了2005年度邵逸夫獎的數學獎。
1637年,費馬在閱讀丟番圖《算術》拉丁文譯本時,曾在第11捲第8命題旁寫道:將一個立方數分成兩個立方數之和,或一個四次冪分成兩個四次冪之和,或者一般地將一個高於二次的冪分成兩個同次冪之和,這是不可能的。關於此,我確信已發現了一種美妙的證法 ,可惜這裡空白的地方太小,寫不下(拉丁文原文: "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.")畢竟費馬沒有寫下證明,而他的其它猜想對數學貢獻良多,由此激發了許多數學家對這一猜想的興趣。數學家們的有關工作豐富了數論的內容,推動了數論的發展。
對很多不同的n,費馬定理早被證明瞭。但數學家對一般情況在首二百年內仍一籌莫展。
1908年,德國佛爾夫斯克宣佈以10萬德國馬克作為獎金獎給在他逝世後一百年內,第一個證明該定理的人,吸引了不少人嘗試並遞交他們的「證明」。在一戰之後,馬克大幅貶值,該定理的魅力也大大地下降。
1983年,Gerd Faltings證明瞭Mordell猜測(Faltings' theorem),從而得出當n > 2時(n為整數),只存在有限組互質的a,b,c使得an + bn = cn。
1986年,Gerhard Frey 提出了“ε-猜想(Epsilon conjecture)”:若存在a,b,c使得an + bn = cn,即如果費馬大定理是錯的,則橢圓曲線:
y2 = x(x - an)(x + bn)
會是谷山-志村猜想的一個反例。 Frey的猜想隨即被Kenneth Ribet證實。此猜想顯示了費馬大定理與橢圓曲線及模形式的密切關係。
1995年,懷爾斯和泰勒在一特例範圍內證明瞭谷山志村猜想,Frey的橢圓曲線剛好在這一特例範圍內,從而證明瞭費馬大定理。
懷爾斯證明費馬大定理的過程亦甚具戲劇性。他用了七年時間,在不為人知的情況下,得出了證明的大部分;然後於1993年6月在一個學術會議上宣佈了他的證明,並瞬即成為世界頭條。但在審批證明的過程中,專家發現了一個極嚴重的錯誤。懷爾斯和泰勒然後用了近一年時間嘗試補救,終在1994年9月以一個之前懷爾斯拋棄過的方法得到成功,這部份的證明與岩澤理論有關。他們的證明刊在1995年的《數學年刊》(Annals of Mathematics)之上。
費馬大定理的證明牽瀕不同範疇的數學學問,主要包括橢圓曲線和模形式。若打算閱讀威爾斯的證明,那應先線上性代數及復分析兩範疇上打好基本功,再轉而閱讀橢圓曲線和模形式的課本。
1676年數學家根據費馬的少量提示用無窮遞降法證明n=4。1678年和1738年德國數學家萊布尼茲和瑞士數學家歐拉也各自證明n=4。1770年歐拉證明n=3。1823年和1825年法國數學家勒讓德和德國數學家狄利克雷先後證明n=5。1832年狄利克雷試圖證明n=7,卻只證明瞭n=14。1839年法國數學家拉梅證明瞭n=7,隨後得到法國數學家勒貝格的簡化……19世紀貢獻最大的是德國數學家庫麥爾,他從1844年起花費20多年時間,創立了理想數理論,為代數數論奠下基礎;庫麥爾證明當n<100時除37、59、67三數外費馬大定理均成立。
為推進費馬大定理的證明,布魯塞爾和巴黎科學院數次設獎。1908年德國數學家佛爾夫斯克爾臨終在哥廷根皇家科學會懸賞10萬馬克,並充分考慮到證明的艱巨性,將期限定為100年。數學迷們對此趨之若鶩,紛紛把“證明”寄給數學家,期望憑短短幾頁初等變換奪取桂冠。德國數學家蘭道印製了一批明信片由學生填寫:“親愛的先生或女士:您對費馬大定理的證明已經收到,現予退回,第一個錯誤出現在第_頁第_行。”
在解決問題的過程中,數學家們不但利用了廣博精深的數學知識,還創造了許多新理論新方法,對數學發展的貢獻難以估量。1900年,希爾伯特提出尚未解決的23個問題時雖未將費馬大定理列入,卻把它作為一個在解決中不斷產生新理論新方法的典型例證。據說希爾伯特還宣稱自己能夠證明,但他認為問題一旦解決,有益的副產品將不再產生。“我應更加註意,不要殺掉這隻經常為我們生出金蛋的母雞。”
數學家就是這樣緩慢而執著地向前邁進,直至1955年證明n<4002。大型電腦的出現推進了證明速度,1976年德國數學家瓦格斯塔夫證明n<125000,1985年美國數學家羅瑟證明n<41000000。但數學是嚴謹的科學,n值再大依然有限,從有限到無窮的距離漫長而遙遠。
1983年,年僅29歲的德國數學家法爾廷斯證明瞭代數幾何中的莫德爾猜想,為此在第20屆國際數學家大會上榮獲菲爾茨獎;此獎相當於數學界的諾貝爾獎,只授予40歲以下的青年數學家。莫德爾猜想有一個直接推論:對於形如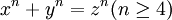 的方程至多只有有限多組整數解。這對費馬大定理的證明是一個有益的突破。從“有限多組”到“一組沒有”還有很大差距,但從無限到有限已前進了一大步。
的方程至多只有有限多組整數解。這對費馬大定理的證明是一個有益的突破。從“有限多組”到“一組沒有”還有很大差距,但從無限到有限已前進了一大步。
1955年日本數學家谷山豐提出過一個屬於代數幾何範疇的谷山猜想,德國數學家弗雷在1985年指出:如果費馬大定理不成立,谷山猜想也不成立。隨後德國數學家佩爾提出佩爾猜想,補足了弗雷觀點的缺陷。至此,如果谷山猜想和佩爾猜想都被證明,費馬大定理不證自明。
事隔一載,美國加利福尼亞大學伯克利分校數學家裡比特證明瞭佩爾猜想。
1993年6月,英國數學家、美國普林斯頓大學教授安德魯·懷爾斯在劍橋大學牛頓數學研究所舉行了一系列代數幾何學術講演。在6月23日最後一次講演《橢圓曲線、模型式和伽羅瓦表示》中,懷爾斯部分證明瞭谷山猜想。所謂部分證明,是指懷爾斯證明瞭谷山猜想對於半穩定的橢圓曲線成立——謝天謝地,與費馬大定理相關的那條橢圓曲線恰好是半穩定的!這時在座60多位知名數學家意識到,困擾數學界三個半世紀的費馬大定理被證明瞭!這一消息在講演後不脛而走,許多大學都舉行了游行和狂歡,在芝加哥甚至出動了警察上街維持秩序。
五十年代日本數學家谷山豐首先提出一個有關橢圓曲線的猜想,後來由另一位數學家志村五郎加以發揚光大,當時沒有人認為這個猜想與費馬大定理有任何關聯。在八十年代德國數學家佛列將谷山豐的猜想與費馬定理聯繫在一起,而安德魯·懷爾斯所做的正是根據這個關聯論證出一種形式的谷山豐猜想是正確的,進而推出費馬最後定理也是正確的。
這個結論由威利斯在1993年的6月21日於美國劍橋大學牛頓數學研究所的研討會正式發表,這個報告馬上震驚整個數學界,就是數學門牆外的社會大眾也寄以無限的關註。不過懷爾斯的證明馬上被檢驗出有少許的瑕疵,於是懷爾斯與他的學生又花了十四個月的時間再加以修正。1994年9月19日他們終於交出完整無瑕的解答,數學界的夢魘終於結束。1997年6月,懷爾斯在德國哥庭根大學領取了佛爾夫斯克爾獎。當年的十萬法克約為兩百萬美金,不過懷爾斯領到時,只值五萬美金左右,但安德魯·懷爾斯已經名列青史,永垂不朽了。
用不定方程來表示,費馬大定理即:當n > 2時,不定方程xn + yn = zn 沒有xyz≠0的整數解。為了證明這個結果,只需證明方程x4 + y4 = z4 ,(x,y) = 1和方程xp + yp = zp ,(x,y) = (x,z) = (y,z) = 1(p是一個奇素數)均無xyz≠0的整數解。
n=4的情形已由萊布尼茨和歐拉解決。費馬本人證明瞭p=3的情,但證明不完全。勒讓德(1823)和狄利克雷(1825)證明瞭p=5的情形。1839年,拉梅證明瞭p=7的情形。1847年,德國數學家庫默爾對費馬猜想作出了突破性的工作。他創立了理想數論,這使得他證明瞭當p<100時,除了p=37,59,67這三個數以外,費馬猜想都成立。後來他又進行深入研究,證明瞭對於上述三個數費馬猜想也成立。在近代數學家中,範迪維爾對費馬猜想作出重要貢獻。他從本世紀20年代開始研究費馬猜想,首先發現並改正了庫默爾證明中的缺陷。在以後的30餘年內,他進行了大量的工作,得到了使費馬猜想成立一些充分條件。他和另外兩位數學家共同證明瞭當p<4002時費馬猜想成立。
現代數學家還利用大型電子計算器來探索費馬猜想,使p 的數目有很大的推進。到1977年為止,瓦格斯塔夫證明瞭p<125000時,費馬猜想成立。《中國數學會通訊》1987年第2期據國外消息報導,費馬猜想近年來取得了驚人的研究成果:格朗維爾和希思—布龍證明瞭「對幾乎所有的指數,費馬大定理成立」。即若命N(x)表示在不超過x的整數中使費馬猜想不成立的指數個數,則證明中用到了法爾廷斯(Faltings)的結果。另外一個重要結果是:費馬猜想若有反例,即存在x>0,y>0,z>0,n>2,使xn + yn = zn ,則x > 101800000.








我已經給出了費馬大定理的初等證明.費馬迷們,請到《光明論壇》去看“一代數學天驕”。雲南富民縣永定鎮劉坤