費馬小定理

出自 MBA智库百科(https://wiki.mbalib.com/)

費馬小定律(Fermat's Little Theorem)

　　費馬小定理是數論中的一個定理。其內容為假如a是一個整數，p是一個質數的話，那麼:

　　a^p = a(mod p)

　　假如a不是p的倍數的話，那麼這個定理也可以寫成:

　　a^{p − 1} = 1(mod p)

　　這個書寫方式更加常用些。

　　費馬小定理是歐拉定理 (數論)的一個特殊情況：假如n和a的最大公約數是1的話，那麼:

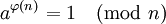
　　在這裡φ(n)是歐拉商數。歐拉商數的值是所有小於n的自然數中與n沒有公約數的數的量。假如n是一個質數，則φ(n) = n-1，即費馬小定理。

　　在費馬小定理的基礎上費馬提出了一種測試質數的演算法。

　　皮埃爾·德·費馬於1636年發現了這個定理，在一封1640年10月18日的信中他第一次使用了上面的書寫方式。在他的信中費馬還提出a是一個質數的要求。這個要求實際上不存在。

　　與費馬無關的有一個中國猜想。這個猜想是中國數學家提出來的。其內容為如果，而且只有當2^p = 2(modp)成立時p才是一個質數。

　　假如p是一個質數的話，則2^p = 2(modp)成立（這是費馬小定理的一個特殊情況）是對的。但反過來，假如2^p = 2(modp)成立那麼p是一個質數是不成立的（比如341符合上述條件但不是一個質數）。因此整個來說這個猜想是錯誤的。

　　一般認為中國數學家在費馬前2000年的時候就已經認識中國猜測了。但也有人認為實際上中國猜測是1872年提出的，認為它早就為人所知是出於一個誤解。

　　若n不整除a-b，x>0，(x,n)=1，則n也不整除x(a-b)。取整數A為所有小於p的集（p不整除A），B為A中所有元素乘以a的集合。因任何兩個A中的元素差都不能被p整除，所以任何兩個B中的元素差也無法被p整除。因此:

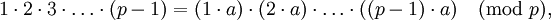
　　即:

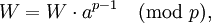
　　在這裡W=1·2·3·...·(p-1)。將整個公式除以W即得到:

　　a^{p − 1} = 1(mod p)

　　如上所述，中國猜測只有一半是正確的，符合中國猜測但不是質數的數被稱為偽質數。

　　假如所有符合1<b<p的b、p都滿足下列條件的話:

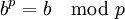
　　則p必定是一個質數。

　　實際上沒有必要測試所有的小於p的自然數，只要測試所有的小於p的質數就可以了。

　　這個演算法的缺點是它非常慢，運算率高。

• 費馬大定理