歐拉定理
出自 MBA智库百科(https://wiki.mbalib.com/)
歐拉定理（Euler Theorem），也稱費馬-歐拉定理或歐拉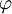
函數定理
目錄 |
歐拉定理指出：如果產品市場和要素市場都是完全競爭的，而且廠商生產的規模報酬不變，那麼在市場均衡的條件下，所有生產要素實際所取得的報酬總量正好等於社會所生產的總產品。該定理又叫做邊際生產力分配理論，還被稱為產品分配凈盡定理。如上所述，要素的價格是由於要素的市場供給和市場需求共同決定。在完全競爭的條件下，廠商和消費者都被動地接受市場形成的價格。現在的問題是：要素所有者按照市場形成的要素價格獲得收入，全部要素收入是否等於社會總產品？
在完全競爭的條件下，廠商使用要素的原則是：要素的邊際產品價值等於要素價格。即：
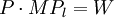（9.9）
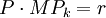（9.10）
由式9.9和9.10可得：
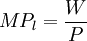（9.11）
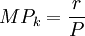（9.12）
P為產品的價格，W/P和r/P分別表示了勞動和資本的實際報酬。因此在完全競爭的條件下，單位勞動、單位資本的實際報酬分別等於勞動、資本的邊際產量。假定整個社會的勞動總量和資本總量為L和K，而社會總產品為Q，那麼就有：
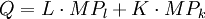（9.13）
式9.13稱為歐拉分配定理。它是由於該定理的證明使用了數學上的歐拉定理而得名。
假設生產函數為：Q=f(L.K)
由於規模報酬不變，所以生產函數為齊次方程，因此有：
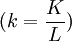
k為人均資本，Q/L為人均產量，人均產量是人均資本k的函數。
![{\partial Q \over \partial L} = {{\partial [ L \cdot \varphi (k) ] } \over \partial L} = \varphi (k) + L \cdot {{d \varphi (k) } \over dk} \cdot {dk \over dL} = \varphi (k) + L \cdot \varphi ^\prime (k) \cdot {dk \over dL} = \varphi (k) + L \cdot \varphi ^\prime (k) \cdot \left( {{-K } \over {L^2} } \right) = \varphi (k) - k \cdot \varphi ^\prime (k)](/w/images/math/5/4/5/5453ffc74dc127601ad904d2a7571fdc.png)
![{\partial Q \over \partial K} = {{\partial [ L \cdot \varphi (k) ] } \over \partial K} = L \cdot {{\partial \varphi (k)} \over \partial k } = L \cdot {{d \varphi (k) } \over dk} \cdot {{\partial k} \over {\partial K}} = L \cdot \varphi ^\prime (k) \cdot {1 \over L } = \varphi ^\prime (k)](/w/images/math/c/5/3/c5381d83bb27cd19a34ae238d7a63815.png)
由上面兩式，即可證明歐拉定理：
![L \cdot {\partial Q \over {\partial L}} + K \cdot {{\partial Q } \over {\partial K}} = L \cdot [\varphi (k) - k \varphi ^\prime (k)] + K \cdot \varphi ^\prime (k) = L \cdot \varphi (k) - K \cdot \varphi ^\prime (k) + K \cdot \varphi ^\prime (k) = L \cdot \varphi (k) = Q](/w/images/math/9/f/5/9f51c0106d39d924e4fb560b1c218437.png)
在規模報酬遞增情況下，如果按照邊際生產力分配，則產品不夠分配給各個生產要素，即：
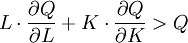（9.14）
在規模報酬遞減情況下，如果按邊際生產力進行分配，則產品在分配給各個生產要素之後還有剩餘，即：
（9.15）
證明如下：
如果生產函數 Q=f(L,K)為r齊次，則有：
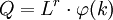
因此有：
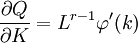
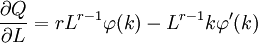
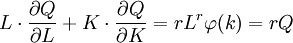
顯然在規模報酬遞增時，r>1，所以有：
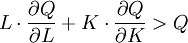
在規模報酬遞減時， ，所以有：
This is very good explanation. Thanks